Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 11
Suponha que seja diferenciável em toda parte. Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.
11.Se for decrescente em , então .
Passo 1
Uma função é dita decrescente quando, em um determinado intervalo, da esquerda pra direita, observamos que o comportamento do gráfico é de “descida”.
Podemos tomar como um exemplo fácil desse caso a função :
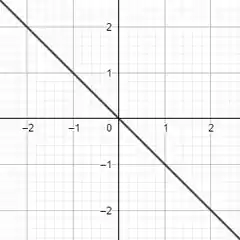
Passo 2
Percebemos que é verdade que o valor de é maior que o de , por sua vez também maior que o de .
E isso, pode confiar, vai valer pra qualquer função que seja decrescente em um intervalo pré-determinado. Logo, a afirmação é verdadeira!
Resposta
Verdadeira.
Exercícios de Livros Relacionados
Seja f x = 2 x - x 2 + 3 , x ∈ R .Verifique que f ' é contínua em R Verifique que f ' x ≠ 0 em R Tendo em vista que f ' 00 , conclua que f é estritamente crescente.(Sugestão: Veja Exercício 13 .)
Se f x = x k , onde k é um inteiro positivo ímpar, prove que f não tem extremos relativos.
Ache a e b , tais que a função definida por f x = x 3 + a x 2 + b Tenha um extremo relativo em 2,3
a ) ache os extremos relativos de f pelo teste da derivada primeira b ) determine os valores nos quais os extremos relativos ocorrem c ) determine os intervalos nos quais f é crescente d ) determine o
A função f é crescente no intervalo I . Prove que a se g x = - f x , então g x será decrescente em I ; b se h x = 1 f x e f x0 em I , então h será decrescente em I .