Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.1 - Ex. 30
Suponha que seja uma função contínua não negativa num intervalo e que , em que é uma constante positiva. Qual será a área entre os gráficos de e ?
Passo 1
Vamos considerar que a função seja , uma função contínua não negativa. Agora, como e tendo em vista que o valor da constante é qualquer número positivo,
Então, a área entre esses gráficos seria, visualmente, assim:
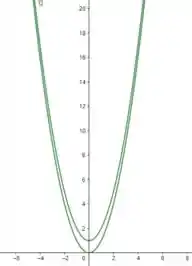
Resumidademente, a área é a intersecção dos pontos entre as curvas e .
Certinho?
Resposta
A área é a intersecção dos pontos entre as curvas e .
Exercícios de Livros Relacionados
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.31 ∫ π 2 π ѳ d ѳ ѳ ѳ
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.35 ∫ 0 1 2 t 2 d t
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.34 ∫ 0 0,3 s 2 d s
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.38 ∫ a 3 a x d x
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.39 ∫ 0 b 3 x 2 d x