Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 44
Suponha que a taxa postal de uma carta seja calculada da seguinte forma: por qualquer peso até os 30 primeiros gramas e então a cada 30 gramas, ou fração adicional, até 330 gramas adicionais. Se for o peso da carta e , expresse a taxa postal como função de x.
Letra a): Faça um esboço do gráfico dessa função.
Letra b): Em quais números do intervalo aberto a função é descontínua?
Letra c): Mostre por que a definição 2.6.1 não é satisfeita em cada descontinuidade da parte b)
Passo 1
Antes de resolver os ites, a questão nos pede para expressar o custo da postagem como função do peso da carta.
Para isso, temos que entender que a postagem tem um preço fixo de até os 30 primeiros gramas e um custo adicional pra cada intervalo de 30 gramas que venha depois. Ou seja, se uma carta tiver de 31 até 60 gramas, paga os primeiros e mais por ter passado de 30, ok?
Passo 2
Assim, nossa função vai ser dada por até termos com um custo de Mas de onde saiu esse 11? Como acho isso?
Então, 12 é o quociente da divisão de 360 por 30, então eu subtraio 1 pois queremos descobrir quantas vezes temos 30 gramas extras, que seriam 1 vez como os primeiros 30 e 11 com os extras.
Matematicamente, temos essa função:
Onde a notação representa o MENOR inteiro MAIOR ou igual a x.
E a parte “” vem para extrairmos o quociente dessa divisão, que nem fizemos ali em cima!
Passo 3
Letra a):
O esboço desse gráfico é uma função escada, que conseguimos definindo a função por partes como no início do passo 2!
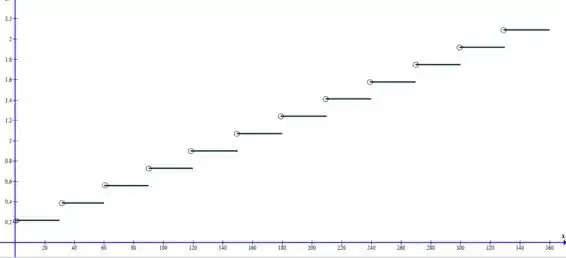
Passo 4
Letra b):
Usando o gráfico feito no passo anterior, vemos que os pontos de descontinuidade são exatamente os múltiplos de 30 entre 0 e 360.
Assim, temos as descontinuidades em
Passo 5
Letra c):
A definição 2.6.1 diz que a função é contínua num ponto sempre que existe e esse limite vale . Mas, pelo gráfico, os limites laterais nesses pontos são distintos, ou seja, não existe limite!
Resposta
Letra a):
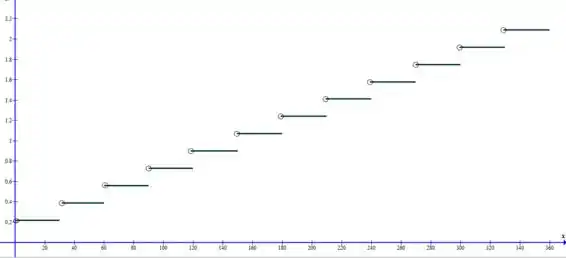
Letra b):
Letra c): Não satisfazem pois os limites laterais são diferentes.