Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 48
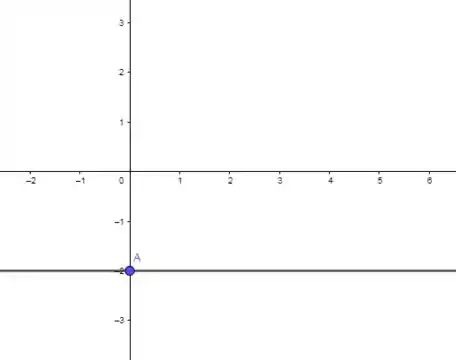
A função f é definida por
Faça um esboço do gráfico de f. Em que valores de x f é descontínua?
Passo 1
Caraca! Essa função foi expressa como um limite!Bem, para obtermos uma equação melhor pra essa função, precisamos descobrir o valor desse limite em termos apenas de x.
Se botarmos ‘n’ em evidência:
Agora é só cortar os ‘n’ e substituir e temos:
Assim, nossa expressão para f é:
Passo 2
Ufa, temos uma expressão sem a variável ‘n’ na equação, então podemos analisar descontinuidade normalmente!Assim, a única restrição que temos é pra , pois não existe
Assim, como não existe o valor de f em 0, a função é descontínua em 0.
Viu? Nem precisamos fazer limite nenhum!
Passo 3
Para fazer o esboço, vamos melhorar essa equação
Sabemos que , então posso cortar o x se fizer uma ressalva de que , por que apenas se o valor de x não é 0.
Assim, nossa função é .
Nosso gráfico então é:
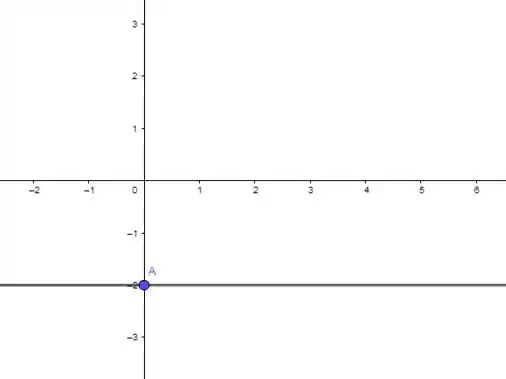
OBS.: não consegui colocar a bolinha aberta em nenhum programa, mas imagina que ela está aberta!
Resposta
