Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 33

O enunciado fornece uma função e pede para que localizemos as descontinuidades da função e esbocemos o seu gráfico.

Então temos que descobrir pontos em que a função tem saltos ou que não está definida. Esses são os pontos de descontinuidade.

Uma boa dica é a gente usar as retrições de e definir o domínio dessa função.

Além disso, vamos utilizar os teoremas mostrados na seção do livro (teoremas 4, 5, 7 e 9).

O teorema 4 afirma que a soma, subtração, produto e quociente de funções contínuas é uma função contínua.
O teorema 5 afirma que todos os polinômios e funções racionais (quociente de polinômios) são funções contínuas em seus domínios.
O teorema 7 afirma que todas as funções raízes, trigonométricas, trigonométricas inversas, exponenciais e logarítmicas são contínuas em seus domínios.
Já o teorema 9 afirma que a composta de funções contínuas é contínua.

O teorema 5 afirma que todos os polinômios e funções racionais (quociente de polinômios) são funções contínuas em seus domínios.
O teorema 7 afirma que todas as funções raízes, trigonométricas, trigonométricas inversas, exponenciais e logarítmicas são contínuas em seus domínios.

Pelos teoremas 5 e 7, e são funções contínuas em seus domínios.

Então vamos achar seus domínios.

Na função exponencial , pode assumir qualquer valor, então não há descontinuidade.

Já em , o denominador da fração não pode ser 0. Então já temos uma descontinuidade em

Assim, pelo teorema 9 (das funções compostas), também é contínua em seu domínio. E pelo teorema 4, a função é contínua em seu domínio.

Consequentemente, como a exponencial é sempre positiva, e, portanto, nunca se anula, é uma função contínua em seu domínio.

Assim, devido ao termo na exponencial, a única descontinuidade de ocorre em

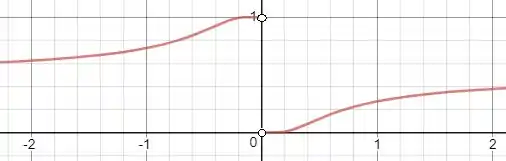
Note no esboço do gráfico de que a função realmente é descontínua em .

R: .