Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.3 - Ex. 60
Suponha que todos os lados de um quadrilátero tenham o mesmo comprimento e que os lados opostos sejam paralelos. Use vetores para demonstrar que as diagonais são perpendiculares.
Passo 1
Vamos imaginar nosso quadrilátero regular , como sendo um quadradinho mesmo, assim:
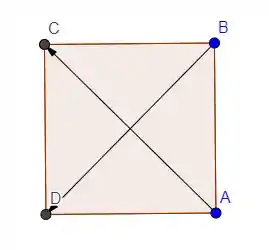
As diagonais dele são dadas pelos vetores
como queremos provar que as diagonais são perpenducilares, devemos provar que o produto escalar entre e é nulo.
Passo 2
Para isso, vamos primeiro definir os vetores diagonal:
E
Show de bola?
Passo 3
Agora vamos ver se o produto escalar dá zero:
E, como a ordem não importa para o produto escalar:
Maaaaas, acontece que todos os lados do quadrilátero tem o mesmo tamanho, Ô SEJE,
Assim,
E o tal do produto escalar deu zero mesmo, quer dizer, os vetores diagonais são perpendiculares
Resposta
Ei, a resposta está no passo a passo :)