Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.2 - Ex. 23 a
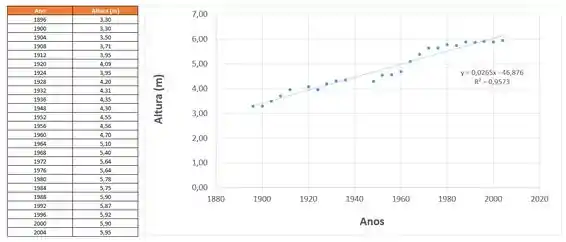
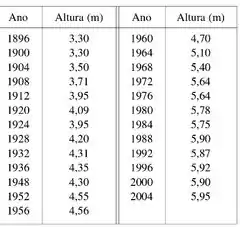
A tabela dá as alturas vencedoras do salto com vara nas olímpiadas de até 2004:
- Faça um diagrama de dispersão e decida se um modelo linear é apropriado.
Passo 1
Eaeee, belezinha!!! Bom... a questão nos dá uma tabela contendo as alturas vencedoras do salto com vara nas olímpiadas de até 2004:
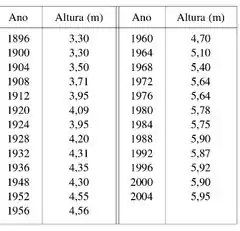
Com essa tabela a questão quer que a gente faça um diagrama de dispersão, ou seja, colocar cada pontinho num gráfico.
E, com esse diagrama, a questão quer que a gente decida se um modelo linear é apropriado, ou seja, se os “pontinhos” podem ser aproximado para uma função de primeiro grau (uma reta).
E aí?? Bora lá?? 😉
Passo 2
Bom... Vamos fazer um gráfico de dispersão, beleza?
Ou seja, para cada ano, vamos colocar um pontinho correspondente à altura.
A melhor forma de fazermos isso é com alguma ferramenta gráfica, porque na mão vai dar um trabaaaaalho.
Usando o Excel, os pontos do enunciado serão:
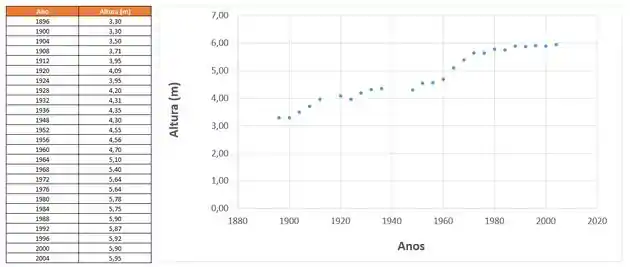
Passo 3
Agora, vamos ver se um modelo linear funciona.
Com a ajuda do Excel vamos tentar aproximar os pontos, através de uma “regressão linear”.
Em outras palavras, vamos aproximar os pontos por uma reta.
Ao fazer isso, temos:
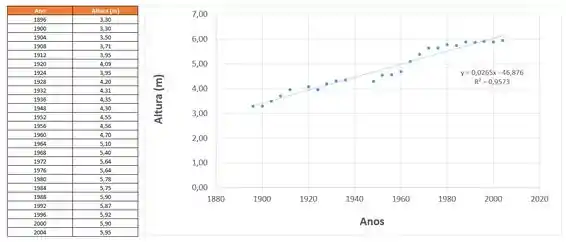
Perceba que os pontos se aproximam bem da reta de equação:
Então o modelo seria apropriado!
Uma forma também de ver se o modelo adequa bem nossos dados é pedir pro nosso software nos dar o valor de , que é a variância!
Quanto mais próximo de esse número for, melhor ajustado estará!
Entendeu direitinho?? Responde aee!!
Resposta
