Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.2 - Ex. 20
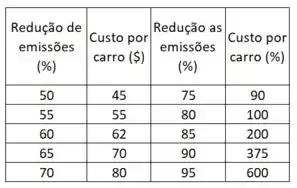
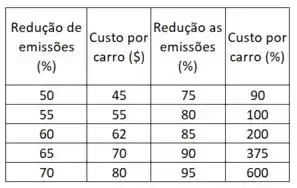
Um estudo do U. S. Office of Science and Technology em estimou o custo para reduzir em certas porcentagens a emissão de poluentes pelos automóveis:
Encontre um modelo que capte a tendência de “rendimentos decrescentes” desses dados.
Passo 1
Opa, bora lá! O problema nos dá uma tabela que relaciona o custo da redução das emissões:
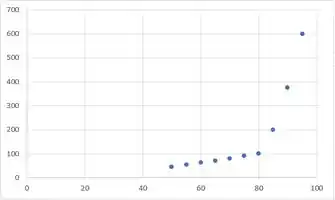
Desejamos encontrar um modelo que capte a tendência dos dados dispostos na nossa tabela e para isso vamos plotar, primeiramente, esses pontos espalhados e tentar observar se eles se assemelham com alguma função que conhecemos.
Depois vamos ver que tipo de curva se aproxima e pra isso vamos usar um software. Depois, com os melhores pontos, podemos calcular os coeficientes necessários.
Passo 2
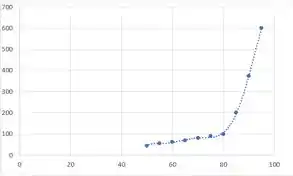
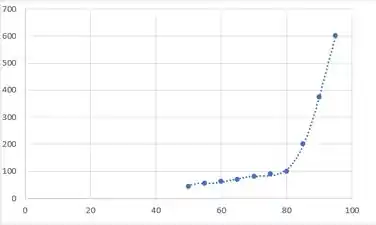
Plotando os pontos, temos:
A partir do gráfico acima e testando as opções presentes no excel de aproximação encontramos que a função que fica melhor aproximada é um polinômio de sexto grau, cuja aproximação fica sendo:
Os polinômios de grau 6 tem a seguinte forma geral:
Onde essas letrinhas são coeficientes, números constantes, que precisamos calcular pra definir o nosso modelo.
E como são 7 incógnitas, precisamos de 7 equações, então vamos escolher 7 pontos do nosso gráfico.
Mas isso tá parecendo muito fácil, porque temos vários.
Sim, a dica tá aqui, esse modelo aproxima os dados, então alguns pontos vão estar bem em cima da curva. Esses são ótimas opções. Outros vão estar mais deslocados, você vai ver que tem um errinho ali. Esses não são boas opções.
Você até pode pegar pontos não tabelados, desde que eles estejam bem em cima da curva.
Passo 3
Os melhores pontos são esses marcadinhos com vermelho:
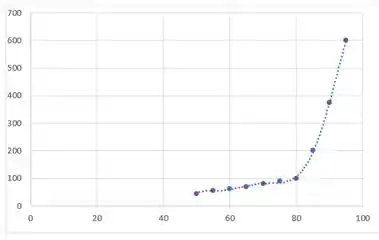
Aqui basta a gente pegar as coordenadas desses pontos e substituir na função. Assim vamos ter um sistema de 6 incógnitas (os coeficientes do modelo) e 6 equações.
Mas vou trazer os coeficientes encontrados pelo software:
Prontinho!
Resposta
