A tabela fornece o número de células de levedura em uma cultura nova de laboratório.
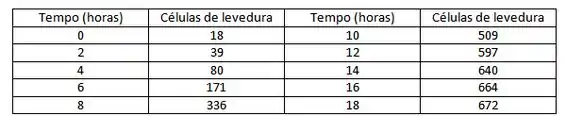
(a) Marque os dados e use o gráfico para estimar a capacidade de suporte para a população de levedura.
(b) Use os dados para estimar a taxa de crescimento inicial relativo.
(c) Encontre um modelo exponencial e um modelo logístico para esses dados.
(d) Compare os valores previstos com os valores observados, na tabela e nos gráficos. Compare como seus modelos se ajustam aos dados.
(e) Utilize seu modelo logístico para estimar o número de células de levedura depois de sete horas.
Passo 1
(a) Bom, galera. A gente tem uma tabela com dados sobre uma cultura de células de levedura e vamos usá-la pra obter mais informações sobre o crescimento dessa cultura.
Primeiro, vamos fazer um gráfico com os pontos dessa tabela:
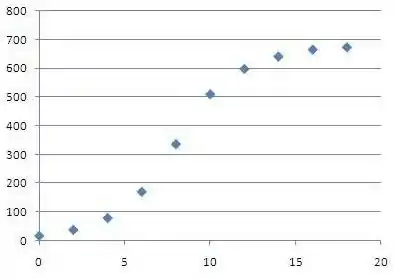
Olhando pro gráfico, dá pra estimar a capacidade de suporte da população, pois o gráfico parece tender para algum número entre e Vamos estimar então que
Passo 2
(b) A taxa de crescimento relativo é dada por . Então, pra estimar a taxa de crescimento inicial relativo, a gente pode calcular uma espécie de derivada desse gráfico, para os pontos iniciais. Mas como a gente faz isso? Não temos nem uma função explícita pra derivar, não é mesmo?
Acontece que a gente pode pegar os primeiros dois pontos, e estimar que a derivada é a inclinação da reta que passa por esses pontos. Vamo lá?
Passo 3
(c) Show! Agora vamos encontrar um modelo exponencial e um modelo logístico para nossos dados. Lembre-se que o modelo exponencial é dado pela seguinte fórmula:
onde é a população inicial e é a taxa de crescimento relativo.
Pela tabela, e, como é constante, podemos usar a taxa de crescimento inicial relativo que estimamos no item anterior, :
Já para o modelo logístico, temos:
No item (a), estimamos , então:
Logo,
Passo 4
(d) Agora vamos comparar os valores observados da tabela com os valores esperados por cada modelo:
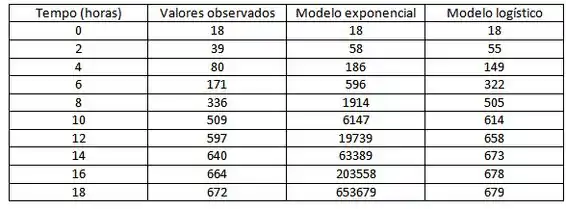
Para visualizar melhor ainda, vamos comparar os três gráficos:
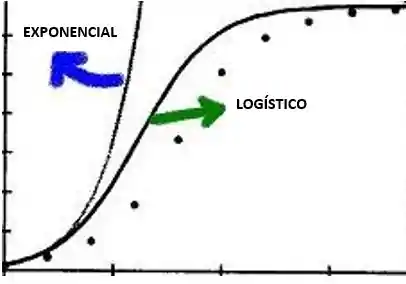
Fica bem visível que o modelo logístico se aproxima muito mais da situação real do que o modelo exponencial, né mesmo?
Passo 5
(e) Depois de sete horas, segundo o modelo logístico, teremos:
Resposta
(a) 80
(b)
(c)
(e)