Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.4 - Ex. 6b
A tabela fornece a população dos Estados Unidos, em milhões, para os anos .
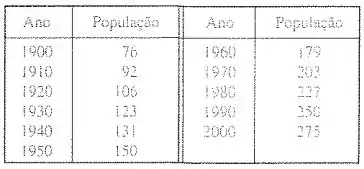
Use o modelo exponencial e os dados do censo para 1980 e 1990 para prever a população em 2000. Compare com a população real. Então uese esse modelo para prever a população nos anos 2010 e 2020.
Passo 1
O exercício fornece uma tabela com a evolução da população americana e pede para aplicarmos um modelo exponencial com as populações de 1980 e 1990 para prever a população em 2000.
O modelo exponencial é do tipo
Devemos achar as constante e . Para isso, usamos que
Assim,
Passo 2
Dividino a primeira equação pela segunda:
Portanto,
Voltando para a primeira equação:
Substituindo o valor de encontrado:
Portanto,
Passo 3
Agora fazemos :
Esse valor é muito próximo do valor real!!! Para os anos seguintes:
Resposta
Exercícios de Livros Relacionados
Nos problemas 41-48, resolva a equação diferencial dada sujeita à condição inicial indicada.48. y ' + 2 y = 1 , no qual y 0 = 5 2 .
Resolva os problemas 1-4 sem consultar o texto. Complete o espaço em branco ou responda verdadeiro ou falso.O problema de valor inicial x y ' = 3 y ,y 0 = 0 possui a solução y = x 3 e_____________.
Resolva y x d y d x = e x ln y sujeito a y 1 = 1 .
Resolva y 2 + 1 d x = ys e c 2 xd y .
Resolva a equação diferencial dada por meio de uma substituição. d y d x + x y 3 s e c 1 y 2 = 0