Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 8
A tabela fornece os valores de uma função obtidos experimentalmente. Use-os para estimar utilizando três subintervalos iguais com (a) extremidades direitas, (b) extremidades esquerdas e (c) pontos médios. Se for sabido que a função é crescente, você pode dizer se suas estimativas são menores ou maiores que o valor exato da integral?
Passo 1
Olá meus queridos.Nessa questão temos uma função e sabemos seus valores em alguns pontos a partir da seguinte tabela:
Queremos calcular a seguinte integral:
E para isso vamos usar o método da soma de Riemann com subintervalos. Na letra a) vamos usar extremidades direitas, na b) extremidades esquerdas e na letra c) pontos médios.
Para começar, vamos rever a fórmula da soma de Rieman,
Com
Onde é o número de subintervalos. é o comprimento de cada subintervalo e são os extremos do intervalo.
é um valor de que pertence ao subintervalo. Na letra a) ele será o ponto extremo direito do subintervalo, na b) o ponto esquerdo e na c) o ponto médio.
Depois devemos dizer se essas estimativas são subestimativas ou superestimativas sabendo que é uma função crescente. Bora lá?
Passo 2
Primeiramente vamos calcular o comprimento dos nossos subintervalos.
Dessa forma, os subintervalos são:
Passo 3
Estimando usando as extremidades direitas:
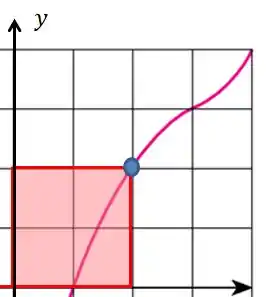
Desde que é crescente, estimar com as extremidades direitas nos dá superestimativas. Isso ocorre pois a área dos retângulos será maior que a área da função. Vou usar um gráfico aqui de uma função crescente pra te mostrar isso:
Passo 4
Estimando usando as extremidades esquerdas:
Desde que é crescente, estimar com as extremidades esquerdas nos dá subestimativas.
Passo 5
Estimando usando os pontos médios:
Nós não podemos dizer nada sobre a estimativa de ponto médio comparado ao exato valor da integral.
Resposta
- , superestimativa
- , subestimativa
- , inconclusivo