Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.2 - Ex. 7
Uma tabela de valores de uma função crescente é dada. Use a tabela para encontrar uma estimativa inferior e superior para .
Passo 1
Fala aí. Tudo certinho com você?
Bom, essa questão dá pra gente a seguinte tabela:
E fala que ela possui valores de uma função crescente é dada.
Teremos que usar essa tabela para encontrar uma estimativa inferior e superior para .
Para isso usaremos a ideia de soma de Riemann, pra isso a gente vai usar essa forma geral aqui:
Onde é dado por:
Como a gente vai pegar os pontos da extremidade de cada intervalo, temos então , que pode ser calculado por:
Na prática, pra fazer o exercício, vamos abrir a integral ali de cima e vamos ficar com:
Passo 2
Vamos começar dando uma olhada nos pontos dessa função:
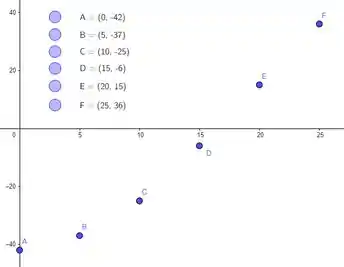
Olha, a gente pode até não saber como, mas sabemos que esses pontos se ligam! E se notarmos bem, vemos que o passo com o qual eles estão distantes é de unidades! Portanto:
E vamos usar isso pra estimar essa integral, beleza? Afinal, uma integral pode ser entendida como a área abaixo da curva! Por estimativa superior, essa integral deve ser algo como a soma da área desses retângulos:
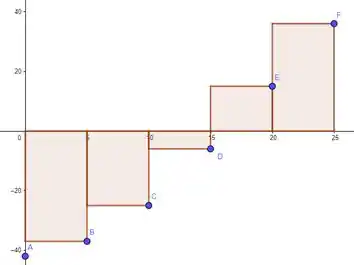
Onde a gente considera “área negativa” pros retângulos abaixo do eixo . Pra estimativa inferior, a ideia é a mesma, mas os retângulos são esses:
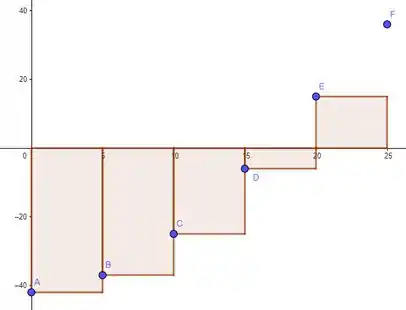
Mesma ideia de “área negativa” aqui também !
Passo 3
Agora é só calcular a área desses retângulos! Em linguagem de Cálculo, isso seria o mesmo que fazer, pra estimativa superior:
E pra estimativa inferior:
E tá na mão!
Resposta
Estimativa inferior:
Estimativa superior: