Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.4 - Ex. 38

O gráfico de y = 4 - | x | e o eixo x de x = - 4 até x = 4 formam um triângulo. Use o método desta secção para encontrar sua área.

Passo 1

A figura com o triângulo se encontra a seguir.

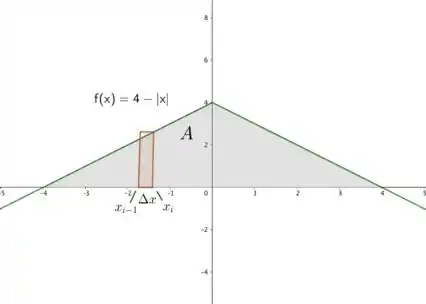
Para calcular a área total do triângulo, nós vamos utilizar a simetria, calculando a área do segundo quadrante e depois multiplicando por 2.

Devemos perceber que no segundo quadrante f x = 4 - - x = x + 4 . E o intervalo da região será [ - 4,0 ] .

Passo 2

Vamos utilizar os retângulos circunscritos para calcular.

Δ x = 0 - ( - 4 ) n = 4 n

f x i = - 4 + i 4 n + 4 = i ⋅ 4 n

A = 2 lim n → + ∞ ⁡ ∑ i = 1 n f ( x i ) Δ x = 2 lim n → + ∞ ⁡ ∑ i = 1 n i ⋅ 4 n 4 n   = 2 lim n → + ∞ ⁡ 16 n 2 ∑ i = 1 n i

Agora vamos usar a fórmula do somatório e calcular o limite.

∑ i = 1 n i ⏞ = I n ( n + 1 ) 2

A = 2 lim n → + ∞ ⁡ 16 n 2 n ( n + 1 ) 2 = 2 lim n → + ∞ ⁡ 8 n n 1 + 1 n = 2 ⋅ 8 1 - 0 = 16

Logo, a área A é 16   u . a .

Resposta

A = 16 ⁡   u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a Regra do Ponto Médio com o valor dado n para aproximar a integral. Arredonde cada reposta para quatro casas decimais. ∫ 2 4 x ln ⁡ x d x ,n = 4
Expresse o limite como uma integral definida no intervalo dado. lim n → ∞ ⁡ ∑ i = 1 n [ 4 - 3 x i * 2 + 6 x i * 5 ] . ∆ x [ 0 ,2 ]
Use a Regra do Ponto Médio com o valor dado n para aproximar a integral. Arredonde cada reposta para quatro casas decimais. ∫ 0 1 sen ⁡ ( x 2 ) d x ,n = 5
Use a forma da definição de integral dada no Teorema 4 para calcular a integral. ∫ 1 4 x 2 + 2 x - 5 d x
Use uma calculadora ou um computador para fazer uma tabela dos valores das somas R n de Riemann à direita para a integral ∫ 0 π sen ⁡ x d x com n = 5 , 10 , 50 e 100 . De qual valor esses números pare