5. Um tanque contém 100 galões de água e 50 onças* de sal. Água contendo uma concentração de sal de (¼) [1 + (½)sent] onças por galão entra no tanque a uma taxa de 2 galões por minuto, e a mistura sai do tanque à mesma taxa.(a) Encontre a quantidade de sal no tanque em qualquer instante. (b) Desenhe o gráfico da solução por um período de tempo longo o suficiente para que vocêveja o comportamento final do gráfico.(c) O comportamento da solução para períodos longos de tempo é uma oscilação em torno deum nível constante. Qual é esse nível? E qual é a amplitude da oscilação?

Graficamente podemos ver que a função começa a oscilar em torno do ponto com uma amplitude de 1 unidades como podemos observar abaixo

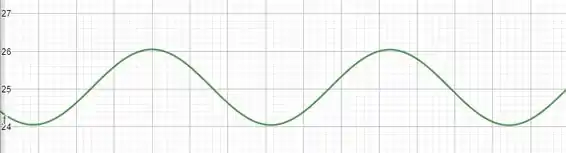
Podemos descobrir isso algebricamente

Analisando esse limite temos o seguinte comportamento

Então por mais que tenhamos uma função seno, o denominador vai impedir que ela seja expressiva no comportamento geral, logo basicamente temos uma função cosseno deslocada 25 unidades para cima

Terminamos por aqui. Te vejo na próxima resolução

: )