Um tanque reservatório de água tem o formato de um cilndro com diâmetro de . Ele está montado de forma que as secções transversais circulares são verticais. Se a profundidade da água é pés, qual é a porcentagem da capacidade total está sendo usada?
Passo 1
Vamos começar fazendo um desenho para representar a situação:
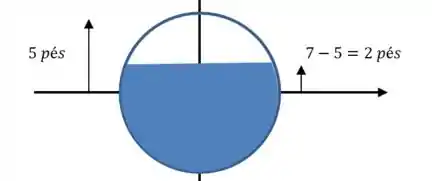
Queremos calcular a porcetangem pintada da área desse círculo, já que a proporção da área ocupada será a mesma do volume.
Passo 2
Para calcular a área desse círculo, precisamos de uma função para ele. Nesse caso, é melhor pegar a seguinte função:
Que dá a metade direita do círculo:
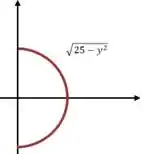
Podemos integrar essa função quando varia de até para encontrar a área ocupada por água. E depois é só multiplicar por dois para levar o outro lado em consideração!
Passo 3
Então vamos fazer a integral:
Como precisaremos fazer substiuições de variável, vamos deixar sem os limites de integração por enquanto.
Vamos aplicar uma substituição:
E lembrando que :
Passo 4
E agora só precisamos resolver essa integral de . Temos que usar uma substituição:
Então:
Substituindo de volta na integral de cima:
Agora precisamos “desfazer” as nossas substituições:
Então:
E para substituir o , precisamos usar uma identidade trigonométrica:
E lembrar que :
Então:
Passo 5
Agora sim, podemos substituir os limites de integração. Tínhamos variando de até :
Essa é a área que está prenchida pela água. A água total do círculo é:
Então a porcentagem de área ocupada é:
Resposta
Está sendo usada da capacidade total.