Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.10 - Ex. 16j
Usando uma ferramenta gráfica, construir o gráfico das funções seguintes, analisando suas propriedades e características como apresentado no item
Passo 1
Vamos ver o que pede esse item :
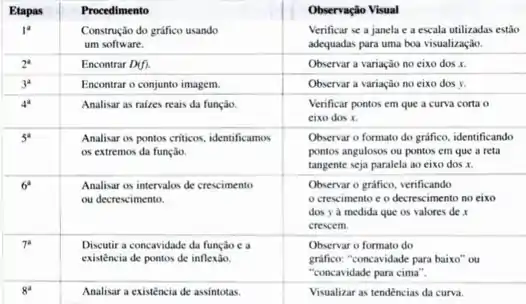
Beleza, a gente tem que aplicar todas essas etapas aí na nossa função.
Passo 2
O gráfico esboçado no Geogebra:
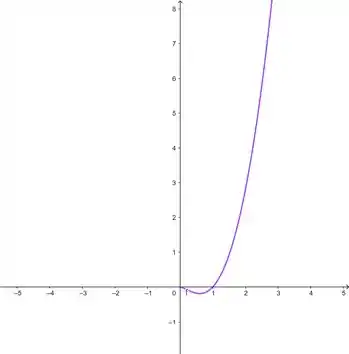
Passo 3
Vamos para as outras etapas agora:
- 2ª: Domínio: o domínio aqui é só o eixo positivo do .
- 3ª: Imagem: A imagem aqui é do mínimo em diante (o mínimo é aproximadamente )
- 4ª: Só tem uma raiz, que é .
- 5ª: Temos um ponto mínimo em (aproximadamente)
- 6 ª: A função é decrescente em e crescente em
- 7ª: Se a gente ampliar um pouco a função, a gente percebe que ela muda a concavidade mais ou menos em :
- 8ª: A função não possui assíntotas.
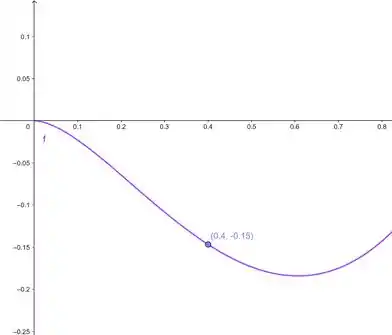
E esse é o ponto de inflexão.
Resposta
Raiz:
Extremos: Ponto mínimo em
A função é decrescente em e crescente em
Concavidade para cima em e para baixo . Ponto de inflexão em
Assíntotas: não tem.
Exercícios de Livros Relacionados
Esboce o gráfico de uma função que satisfaça todas as condições dadas. f ' 0 = f ' 2 = f ' 4 = 0 , f ' x0 se x0 ou 2x4 , f ' x0 se 0x2 ou x4 , f ' ' x0 se 1x3 , f ' ' x0 se x1 ou x3
Esboce o gráfico de uma função que satisfaça todas as condições dadas. f ' 1 = f ' - 1 = 0 , f ' x0 se x1 , f ' x0 se 1x2 , f ' x = - 1 se x2 , f ' ' x0 se - 2x0 E ponto de inflexão em 0,1
Esboce o gráfico de uma função que satisfaça todas as condições dadas. f ' x0 se x2 , f ' x0 se x2 , f ' - 2 = 0 , lim x → 2 f ' x = ∞ , f ' ' x0 se x ≠ 2
Esboce o gráfico de uma função que satisfaça todas as condições dadas. f ' x0 se x2 , f ' x0 se x2 , f ' 2 = 0 , lim x → ∞ f x = 1 , f - x = - f ( x ) f ' ' x0 se 0x3 f ' ' x0 se x3
Esboce o gráfico de uma função que satisfaça todas as condições dadas. f ' x0 e f ' ' x0 para todo x .