Determine os sinais das derivadas parciais da função cujo gráfico está mostrado.
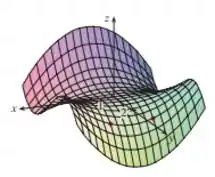
(a)(b)
Passo 1
Fala aí, galera! Beleza?
Nessa questão nós temos o gráfico de uma função e queremos responder se as derivadas segundas no ponto dado são positivas ou negativas, ok?
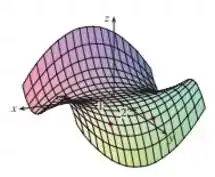
Bom, aqui nós temos derivadas cruzadas. Vamos entender melhor como analisar...
A derivada primeira representa a taxa de variação de quando está fixado. Outra forma de entender isso é pensar que é a inclinação da reta tangente ao gráfico de quando fixamos um certo valor de .
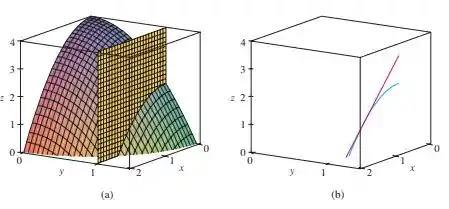
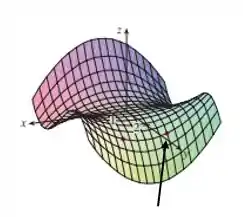
Veja a imagem acima, retirada do livro James Stewart, Cálculo Vol. 2. Na figura (a), podemos ver um plano que define para uma função qualquer.
A derivada corresponde à inclinação da reta tangente ao gráfico de nos pontos . Na figura (b) ao lado, essa reta tangente (em cor rosa) é mostrada para algum ponto .
Sendo assim, a derivada segunda de vai nos dar a taxa de variação da derivada primeira, ou seja, a taxa de variação da inclinação da reta tangente ao gráfico de quando mantemos constante
Tá comigo até aqui? Vamos seguir então...
Passo 2
O que significa a derivada segunda? Ora, dará a taxa de variação da derivada primeira, ou seja, a taxa de variação da inclinação daquela reta rosa.
Se a inclinação da reta rosa aumenta conforme aumenta, então a inclinação será uma função crescente e será positiva, significando uma concavidade para cima, por exemplo.
Perfeito! Agora nós entendemos o significado da derivada segunda.
Mas como podemos analisar Essa derivada pode ser escrita como
Ou seja, uma vez que sabemos a inclinação para algum ponto , como na imagem (b), será a taxa de variação da inclinação quando variamos . Ela vai nos dizer o que acontece com aquela reta rosa conforme variamos .
Bom, com isso nós podemos analisar e.
Partiu?
Passo 3
Vamos começar por
Como discutimos antes, primeiro nós vamos encontrar
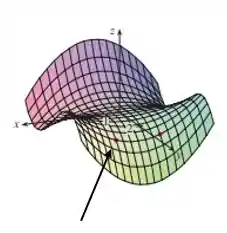
Podemos ver que a função tem inclinação positiva no ponto . Para responder sobre vemos que a inclinação aumenta quando passamos a olhar para ela em valores maiores de Logo, podemos dizer que é positivo!
Passo 4
Da mesma forma, vamos analisar o ponto
Nesse caso, vemos que a inclinação da reta nesse ponto é negativa. Conforme nos deslocamos para valores maiores de , essa inclinação se torna cada vez mais negativa, ou seja, é decrescente. Com isso, podemos dizer que �� negativo.