Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.1 - Ex. 103

Uma terna de inteiros positivos a,b e c é chamada terna pitagórica se a 2 + b 2 = c 2 . Seja a um inteiro positivo impar e sejam

b = a 2 2             e                 c = a 2 2

Respectivamente, o piso inteiro e o teto inteiro para a 2 2

a) mostre que a 2 + b 2 = c 2 . (sugestão :; considere que a = 2 n + 1 e expresse b e c em termos de n.)

b) por cálculo direto, ou com auxílio da figura, encontre

lim a → ∞ ⁡ a 2 2 a 2 2

Passo 1

Falaaaaa rapaziada tudo blz? Repare o desenho representativo dado na questão,

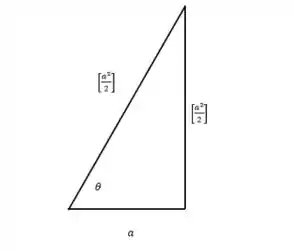
Na letra (a) vamos ter que,

Se a = 2 n + 1 então,

b = a 2 2 = 4 n 2 + 4 n + 1 2 = 2 n 2 + 2 n + 1 2 = 2 n 2 + 2 n  

Com isso c = a 2 2 = 2 n 2 + 2 n + 1 2 = 2 n 2 + 2 n + 1

a 2 + b 2 = 2 n + 1 2 + 2 n 2 + 2 n 2 = 4 n 2 + 4 n + 1 + 4 n 4 + 8 n 3 + 4 n 2 = 4 n 4 + 8 n 3 + 8 n 2 + 4 n + 1 = 2 n 2 + 2 n + 1 2 = c 2

Passo 2

Já na letra ( b ) temos que ,

lim a → ∞ ⁡ a 2 2 a 2 2 = lim a → ∞ ⁡ 2 n 2 + 2 n 2 n 2 + 2 n + 1 = 1 ,       ou lim a → ∞ ⁡ a 2 2 a 2 2 = lim a → ∞ ⁡ sin ⁡ θ = lim θ → π 2 ⁡ sin ⁡ θ = 1

Resposta

a) c 2

b) 1

Exercícios de Livros Relacionados

Determine se a sequência converge ou diverge. Se ela converge, encontre o limite.26. a n = 2 + ( 0.86 ) n
Determine se a sequência converge ou diverge. Se ela converge, encontre o limite.27. a n = 3 n 7 - n
Encontre uma fórmula para o termo geral a n da sequência, assumindo que o padrão dos primeiros termos continue. 4 , - 1 , 1 4, - 1 16 , 1 64 , …
Determine se a sequência converge ou diverge. Se ela converge, encontre o limite.39. a n = { s e n n }
Determine se a sequência converge ou diverge. Se ela converge, encontre o limite.24. a n = 3 + 5 n 2 1 + n