Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.1 - Ex. 39
Determine se a sequência converge ou diverge. Se ela converge, encontre o limite.
39.
Passo 1
Fala galera, tudo bem? O problema nos deu essa sequência aqui
E precisamos decidir se ela converge ou diverge. E se convergir, vamos encontrar seu valor. E agora? É através do limite!
Precisamos aplicar o limite sobre essa sequência, para vermos se ela converge ou diverge.
Se ela converge, o limite acima é um número que chamaremos de .
Beleza? Vamos resolver juntos?
Passo 2
Temos nosso limite
Sabemos que são números inteiros positivos, além disso, sabemos algo sobre a função seno?
Sim! Ela é uma função que aceita todos os , mas sua imagem está limitada a valores entre .
E agora?
Passo 3
Fazendo um gráfico (de ) da função (sua versão contínua, mas assim podemos ter uma noção da nossa sequência) temos
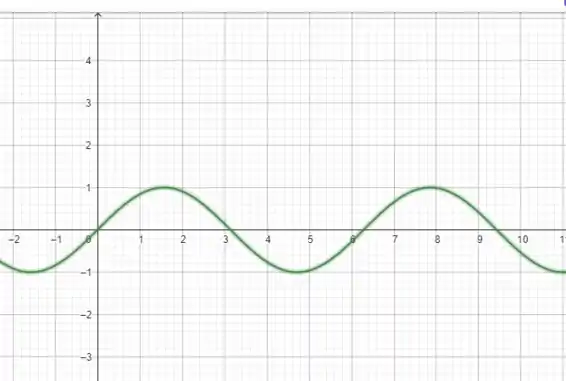
Mas como podemos ver, a função seno resulta em valores entre -1 e 1, então, ao aplicarmos o limite, não irá convergir (mesmo a sequência sendo limitada por -1 e 1), já que ela não é monótona.
Então ela será divergente.