Explique a diferença entre mínimo local e mínimo absoluto.
Passo 1
Fala aí, tudo belezinha com você?
Bem, esse exercício pede para gente explicar a diferença entre um mínimo local de um mínimo absoluto.
E para responder a essa questão precisaremos lembrar de alguns conceitos importantes sobre derivadas e extremos de intervalos de funções.
Vem comigo que te explico tudinho no passo a passo.
Passo 2
Para entender a diferença vamos usar a seguinte figura:
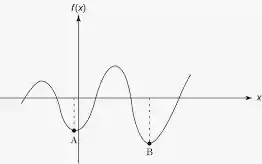
Observe que temos dois lugares diferente onde a função está descendo e faz uma curva e volta a subir. Isso acontece nos pontos e .
Para esses casos dizendo que esse pontos são pontos de mínimos locais. Pois olhando localmente a função assume um valor mais baixo em relação ao seus arredores.
Isso pode ser encontrado procurando da derivada da função tem inclinação igual a zero naquela região.
Olhando para toda a função podemos ver que tem um valor menor que , e que qualquer outro ponto da função. Ou seja, representa um mínimo global.
Passo 3
Agora se estivéssemos analisando apenas a região vermelha da função. Encontrariamos apenas , e seria um mínimo. Ou seja, trata-se de um minimo local, pois temo um intervalo que não contem . Como mostrado abaixo:

Formalmente dizemos que: um mínimo local é um ponto tal que:
Para todo em uma vizinhaça de , enquanto que um mínimo absoluto (ou global) é um ponto tal que:
Para todo no domínio da função.
Resposta
Explicação.