Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 37
Se um topógrafo mede as diferenças nas elevações dos terrenos em um deserto, com a finalidade de construir uma rodovia, ele tem de fazer correções por causa da curvatura da Terra.
(a) Se é o raio da Terra e , o comprimento da rodovia, mostre que a correção a ser feita será
(b) Use um polinômio de Taylor para mostrar que
(c) Compare as correções dadas pelas fórmulas em (a) e (b) para uma rodovia que tenha de percurso. (Tome o raio da Terra como .)
Passo 1
E aí, meus amigos! Tudo tranquilo?
Nossa questão traz uma situação onde um topógrafo mediu as elevações de um terreno e precisa corrigir esses valores devido à curvatura da Terra.
A parte a) pede para mostrarmos que a essa correção deve ser feita usando a equação:
Pra chegar nessa expressão, vamos usar correlações trigonométricas com base na imagem que o enunciado nos forneceu.
A parte b) pede para usarmos um polinômio de Taylor para mostrar que o valor da correção é:
Como no passo a) vamos ter encontrado expressa pela função secante, vamos partir do polinômio de Taylor para essa série para chegarmos na nossa equação desejada.
Por último, a parte c) pede para calcularmos as correções usando as equações de a) e de b).
Vamos passo a passo!
Passo 2
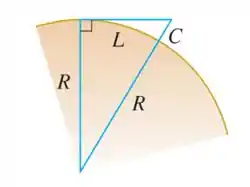
(a) Para chegarmos à expressão da correção, olhe bem pra figura:
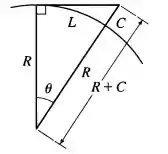
Veja que é o comprimento do arco subentendido pelo ângulo . Como a equação pro comprimento do arco é dada pelo ângulo interno do arco multiplicado pelo comprimento do raio do arco , para o nosso caso, teremos:
Isolando :
A função secante é o inverso da função cosseno, temos que:
Então, para o nosso retângulo, temos:
Isolando :
Substituindo o valor de que achamos anteriormente:
Pronto! Chegamos na equação que a letra a) pede.
Passo 3
(b) Vamos usar um polinômio de Taylor para expressar :
Como na expressão do item a), temos os termos , vamos fazer no polinômio :
Substituindo os termos de com :
Simplificando, chegamos na aproximação desejada:
Passo 4
(c) Substituindo e na fórmula do item (a), obteremos
Mas, se usarmos a aproximação do item (b), teremos:
Subtraindo esses dois valores, teremos uma diferença de:
Resposta
(c) Diferença de: .