Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.1 - Ex. 20
Prove que o comprimento do latus rectum de uma parábola é .
Passo 1
A questão pede para provarmos que o comprimento do latus rectum de uma parábola é . Para isso, precisamos lembrar que o latus rectum é a corda que passa pelo foco e é perpendicular ao eixo da parábola, como ilustrado na figura:
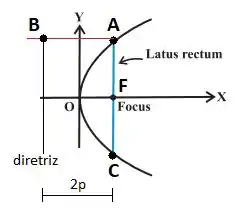
Queremos achar o comprimento .
Passo 2
Para resolver esse problema, vamos usar a propriedade fundamental da parábola: a distância do foco a um ponto da parábola é igual a distância desse ponto à reta diretriz. Desta forma, temos que
Por outro lado, sabemos que a distância . Como é paralelo a , temos que a distância . Assim, temos que
Desta forma,
Resposta
Demonstração.
Exercícios de Livros Relacionados
Nos Exercícios de 33 a 40, ache uma equação da parábola com as propriedades dadas. Faça um esboço do gráfico.37. Vértice em ( 3 ,- 2 ) ; eixo x = 3 ; comprimento do latus rectum é 6.
50. Se uma parábola tiver seu foco na origem e o eixo x como eixo, prove que ela deve ter uma equação da forma y 2 = 4 k x + 4 k 2 ,k ≠ 0 .
52. Mostre que após uma translação de eixos para a nova origem - 1 4 π ,1 a equação y = 1 2 s e nx + cos x + 1 torna – se y ' = s e nx '
48. Na Figura 16, prove que α = β . (Sugestão: escolha os eixos coordenados de tal forma que a parábola tenha seu vértice na origem e seu eixo ao longo do eixo y e que se abra para cima. Seja Q a inte
43. O cabo de uma ponte suspensa tem a forma de uma parábola quando a carga é uniformemente distribuída na horizontal. A distância entre duas colunas é 150 m, os pontos de suporte do cabo nas colunas