Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 28
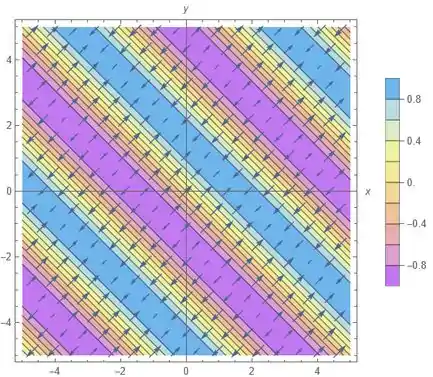
Trace o campo vetorial gradiente de e o mapa de contorno de . Explique como eles estão relacionados.
Passo 1
Faala, galera! Tudo certo?
Essa questão nos deu uma função de duas variáveis:
E pediu pra desenharmos o campo vetorial gradiente e o mapa de contorno dela! Pra isso, vamos usar um software, que no nosso caso vai ser o Mathematica.
O campo gradiente nós vamos calcular, que é assim:
Feito o desenho, vamos ver como se relaciona o mapa de contorno com o campo.
Passo 2
Primeiro, vamos achar as derivadas parciais de .
Em função de , com constante:
E em função de , considerando constante:
Então nosso gradiente é:
Passo 3
Pra plotar isso no Mathematica, vamos usar três comandos:
- VectorPlot para desenhar o campo vetorial
- ContourPlot para desenhar o mapa de contorno
- Show para mostrar os dois desenhos ao mesmo tempo
Juntando os três fica assim:
Precisamos colocar alguns componentes dentro do comando pra deixar o gráfico mais fácil de ver.
O retorno do software é esse aqui:
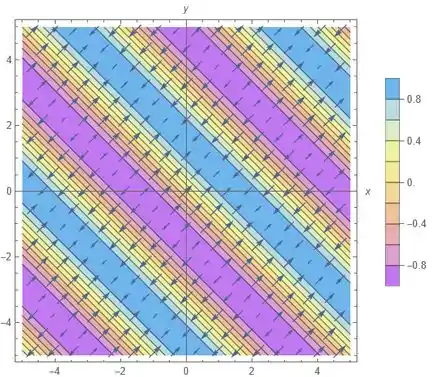
Passo 4
Agora analisamos esse desenho pra ver a relação entre os dois.
Bom, percebe que os vetores apontam sempre no sentido da região rosa para a região azul. Se olharmos pra legenda, isso quer dizer que os vetores estão na direção de crescimento de .
Além disso, enquanto os vetores são paralelos a , as curvas de nível são paralelas a , ou seja, eles são perpendiculares!
Resposta
