Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.1 - Ex. 26
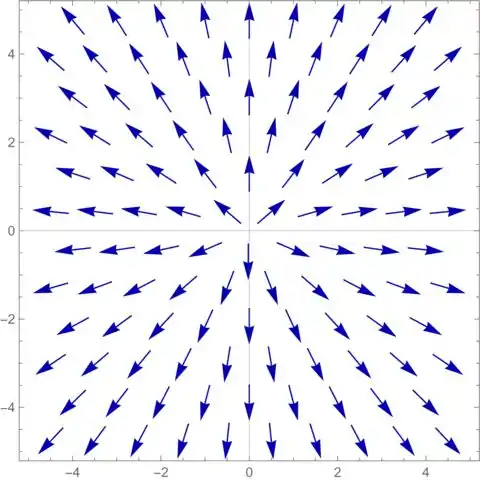
Determine o campo vetorial gradiente de e o esboce.
Passo 1
E ai, pessoal, tudo certo? Vamos dar uma olhada nessa questão!
Precisamos calcular o campo gradiente da função
E depois esboçar.
Pra isso, vamos lembrar que o gradiente é calculado assim:
Então começamos calculando as derivadas parciais pra definir esse campo.
Com ele definido vamos estudar como ele se comporta conforme mudamos os valores de e . Vamos também analisar o tamanho do vetor em cada ponto, que é calculado assim:
Assim, conseguimos desenhar os vetores em alguns pontos, pra representar o campo vetorial!
Passo 2
Pra calcular as derivadas parciais, quando derivamos em função de uma das variáveis, a outra é constante.
Primeiro em função de , com constante:
Usando a regra da cadeia, calculamos:
De forma análoga, derivamos em função de , com constante:
Usando a regra da cadeia:
Ou seja,
Ou
Uma primeira observação importante é que o campo não está definido para , já que nesse ponto o denominador vale , o que não pode acontecer!
Passo 3
Calculando a norma:
Ou seja, independente de , temos que:
Passo 4
Vamos então analisar o campo vetorial:
Percebe que o denominador das duas componentes é sempre positivo (), o que faz com que o numerador defina o sinal. Ou seja, o sinal de e vão definir pra onde o vetor aponta:
- Se , o vetor aponta pro sentido positivo de
- Se , o vetor aponta pro sentido negativo de
- Se , o vetor é perpendicular ao eixo
E o mesmo vale para . Em resumo:
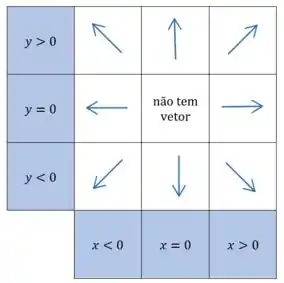
Na prática, é como se os vetores estivesse se “afastando” da origem.
Vamos desenhar alguns pra representar o campo:
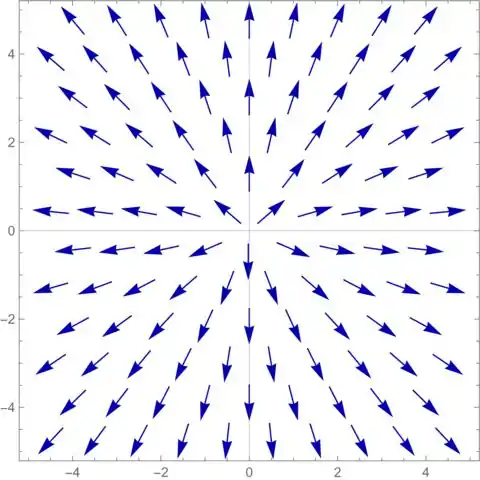
Resposta
