Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 18
Faça a correspondência entre o campo vetorial em e a figura rotulada de . Justifique suas escolhas.
Passo 1
E ai pessoal, beleza? Bora lá!
Temos um campo vetorial e devemos identificar qual figura de que o representa, justificando a escolha.
Como podemos resolver?
Repare no campo vetorial:
Vamos considerar a hipótese de , e assumirem valores positivos, certo? É apenas uma hipótese para facilitar a resolução.
Fazendo isso, sempre teremos vetores apontados para longe da origem, com magnitude que aumenta à medida que se afastam da origem.
Com essa informação podemos analisar as figuras e ver qual apresenta este comportamento.
Vamos lá!!!
Passo 2
Vamos assumir uma hipótese: as componentes , e do campo vetorial irão assumir valores positivos.
Quando a gente faz isso, repare que à medida que vamos aumentando os valores de , e sempre teremos vetores apontados para longe da origem, com uma magnitude que aumenta à medida que se afastam da origem.
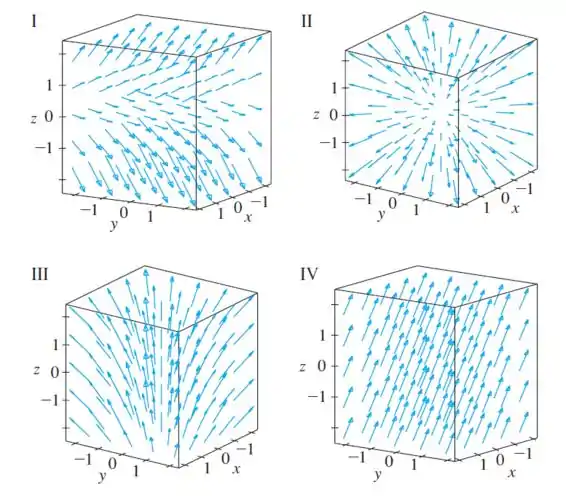
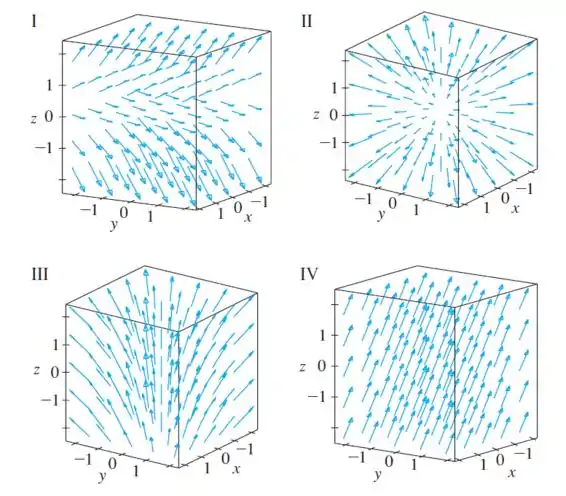
Analisando as figuras:
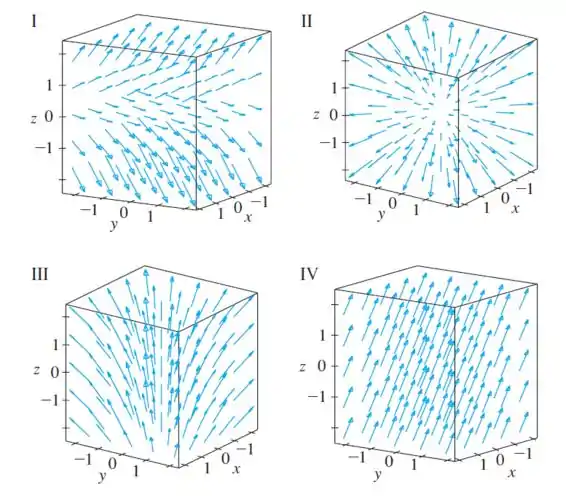
Foque na figura , pois ela apresenta exatamente esse comportamento. Na origem o vetor é zero, e na medida que se afastamos da origem os vetores aumentam de tamanho conforme falamos antes.
Logo, podemos concluir que a figura representa nosso campo vetorial.
Resposta
Figura