Se você dispõe de um SCA que trace campos vetoriais (o comando para fazê-lo no Maple é “fieldplot” e no Mathematica é “PlotVectorField” ou “VectorPlot”), use-o para traçar

Explique sua aparência, determinando um conjunto de pontos tal que .

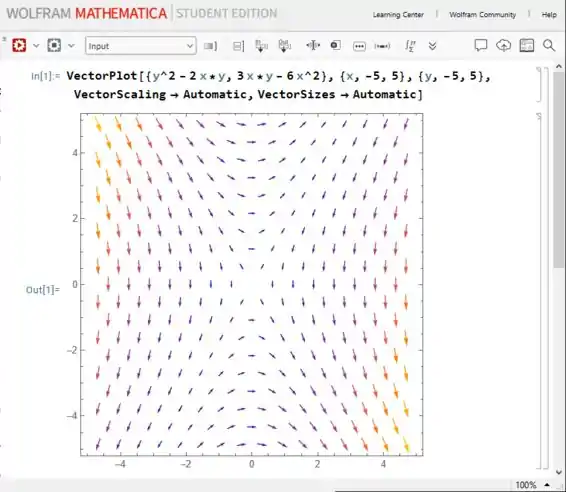
Pra gerar esse campo no Mathematica, vamos usar o comando “VectorPlot”, só que vou colocar mais dois componentes pra ajudar no visual:

VectorScaling Automatic

VectorSizes Automatic

Esses dois atributos, dentro do comando “VectorPlot” deixam o ajuste de tamanho e escala dos vetores automáticos, o que facilita a nossa visualização do campo. Então, o comando e a resposta ficam assim:

Agora vamos ver onde esse campo

Vale zero:

Isso vai acontecer quando as duas coordenadas derem zero:

Analisando a primeira equação:

Quando temos um produto de dois termos igual a zero, temos que um dos dois vale zero, então:

ou

Para a segunda equação:

E de novo:

ou

Para que as duas equações sejam verdade ao mesmo tempo, temos que:

Então são nos pontos que pertencem a essa reta que o campo é nulo.

Por último, vamos analisar o campo.

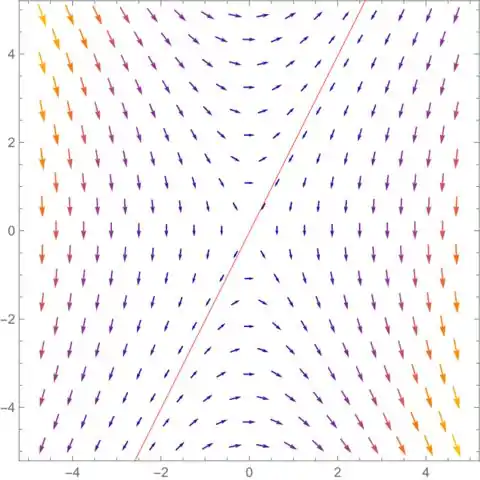
Essa reta vermelha é a reta . Como nela o campo é nulo, não tem nenhum vetor que parte dela!

Percebe que ela divide o campo:

Considerando os vetores mais próximos dela, de um lado os vetores apontam pra uma direção e do outro lado pra outra.

Isso tem a ver com as expressões das coordenadas do campo:

Acima da reta , temos que , e, portanto,

Já abaixo, temos o oposto: e

Isso faz com que, com pouca alteração no valor de (por isso perto da reta), os sinais das coordenadas do vetor se invertem! E então o vetor muda de direção.