Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 4
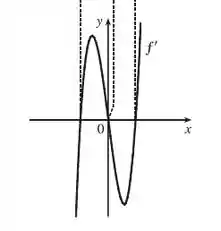
Trace ou copie o gráfico da função dada. (Suponha eixos com a mesma escala.) Use então o método do Exemplo para esboçar o gráfico de .
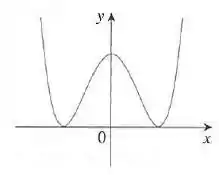
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente traçar o gráfico da derivada da função, usando o próprio gráfico da função.
Pra isso, ele pediu pra gente usar o mesmo método do Exemplo , que consiste em traçar retas tangentes na curva e estimar sua inclinação. Então, é isso que nós vamos fazer, analisando o formato da nossa curva.
Vamos lá!
Passo 2
Primeiro, vamos observar todas as interceptações em no gráfico de , para obter todas as retas tangentes que forem horizontais no gráfio de . Aqui vemos que acontece três vezes:
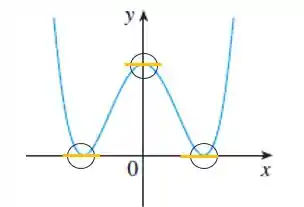
Isso significa que o gráfico da nossa derivada vai cruzar o eixo em cada um desses pontos.
Agora vamos procurar por qualquer pontas ou “bicos” no gráfico de , que possam gerar pontos de descontinuidade no gráfico da derivada .
Repare que a função é contínua em todo domínio, então aqui tudo tranquilo.
Agora, precisamos lembrar que em qualquer intervalo em que tenha uma tangente com inclinação positiva, o gráfio de será positivo, e que quando a inclinação de for negativa, o gráfico de será negativo. Além disso, se o gráfico da função for linear, o gráfico de será uma linha horizontal.
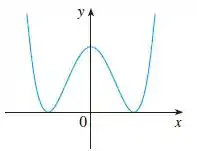
Repare que da esquerda para a direita, o gráfico de tem inclinação negativa. Essa inclinação se torna nula, depois vira positiva de novo até chegar em . Em seguida, depois de passar pelo eixo , temos novamente uma inclinação negativa, seguida de uma inclinação nula (reta horizontal) e termina positiva. Olha só:
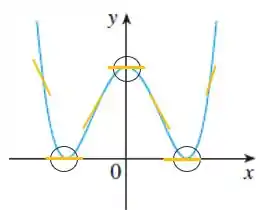
Juntanto todo isso e fazendo a correspondência com o gráfico de , vamos ter o gráfico da nossa derivada logo abaixo:
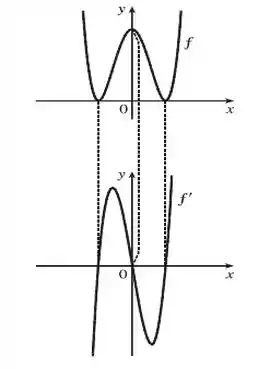
Prontinho, galera! Até a próxima! 😉
Resposta
