Seja .
(a) Estime os valores de , , e fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de .
(b) Use a simetria para deduzir os valores de , e .
(c) Utilize os resultados de (a) e (b) para conjecturar uma fórmula para .
(d) Use a definição de derivada para demonstrar que sua conjectura em (c) está correta.
Passo 1
Fala, galera! Beleza? Bora resolver essa questão!
O enunciado pediu pra gente encontrar a derivada da função nos pontos , , e , usando uma ferramenta gráfica para isso. Além disso, ele pediu pra gente usar a simetria da curva e deduzir os valores das derivadas nos pontos , e .
A partir disso, nós precisamos encontrar uma fórmula para essa derivada, . E por fim, demonstrar que essa fórmula está correta, usando a definição de derivada:
Vamos lá!
Passo 2
Vamos começar esboçando o gráfico da função :
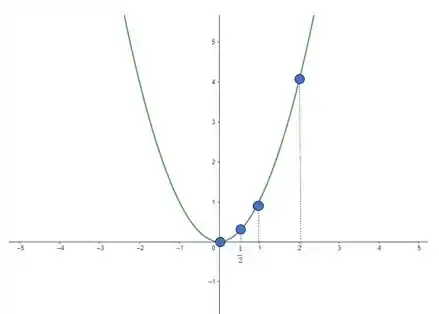
Olha ali nossa bolinhas azuis, indicando os pontos onde , , e , nessa ordem, da esquerda para direita. Esses são nossos pontos de interesse, beleza?
Vamos dar um zoom nessa parte:
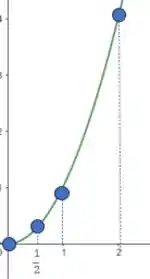
Repare que em , a reta tangente nesse ponto seria horizontal, ou seja, teria inclinação zero. Isso quer dizer que a nossa derivada nesse ponto é dada por:
Agora para estimar o valor da derivada no ponto , vamos a inclinação da tangente nesse ponto, que parece ser aproximadamente . Então, temos:
Da mesma forma, a inclinação da tangente no ponto , parece ser aproximadamente . Então, temos:
Por fim, para , conseguimos estimar uma inclinação na reta tangente de aproximadamente . Logo:
Essas são estimativativas baseadas apenas na interpretação visual do gráfico, como o item (a) nos pediu.
Passo 3
Agora no item (b), ele pediu pra gente usar a simetria do gráfico para estimar a derivada nos pontos , e .
Olhando para o gráfico que desenhamos no passo , da função , a gente percebe que é espelhada em relação ao eixo . Isso significa que o tem de um lado é igual ao que tem do outro, só muda o sinal, que passa a ser negativo.
Isso se aplica também as inclinações da retas tangentes nos pontos considerados, então também podemos estimar as derivadas, como fizemos no passo anterior, para obter por simetria:
Isso acontece porque .
Passo 4
Agora para para conjecturar uma fórmula para , vamos analisar os resultados dos passos anteriores. Olha só:
O mesmo acontece quando é negativo. Percebeu que a derivada tá dobrando o valor de ? Isso significa que a gente pode conjecturar uma fórmula onde está sendo multiplicado por , ou seja:
Passo 5
Agora vamos verificar se essa conjectura está correta, usando a definição de derivada:
Para e , temos:
Expandindo o termo ao quadrado:
Simplificando:
Colocando em evidência e simplificando novamente:
Assim, quando vai pra zero, temos:
Mostrando que a nossa conjectura estava correta.
Valeu, galera! Até a próxima! 😉
Resposta
a) , , ,
b) , , ,
c)
d)