Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 10
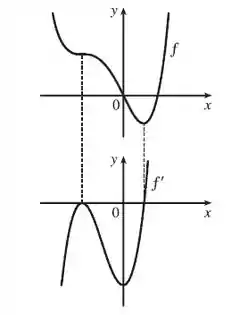
Trace ou copie o gráfico da função dada. (Suponha eixos com a mesma escala.) Use então o método do Exemplo para esboçar o gráfico de .
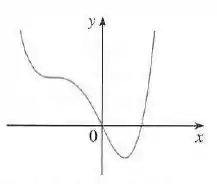
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
A partir do exemplo 1 do livro, iremos aqui construir o gráfico da derivada da função, a partir do gráfico da função.
Primeiro, vamos plotar todas as interceptações em no gráfico de para todas as tangentes que forem horizontais no gráfio de , aqui vemos que acontece duas vezes.
Agora vamos procurar por qualquer pontas no gráfico de , se tiver, haverá uma descontinuidade no gráfico de , aqui não temos nenhuma.
Passo 2
Em qualquer intervalo em que tenha uma tangente com inclinação positiva, o gráfio de será positivo, e com inclinação negativa, o gráfico de será negativo, e se o gráfico da função for linear, o gráfico de será uma linha horizontal.
Vemos que aqui, da esquerda para a direita, o gráfico de tem inclinação negativa, se torna , volta a ser negativa, chega em de novo e por fim termina positiva.
Passo 3
1. Da esquerda do ponto A, as inclinações das retas tangentes são inicialmente muito negativas e depois se tornam menos negativas até atingirem a horizontal (0) no ponto B. Isso significa que a derivada começa negativa e se move em direção a 0 à medida que nos aproximamos do ponto B.
2. Do ponto A ao ponto C, a taxa de diminuição aumenta, e as inclinações tangentes começam a se tornar mais negativas. Portanto, se move para baixo afastando-se de 0.
3. No ponto C (diretamente acima do ponto D), as inclinações tangentes começam a se tornar menos negativas novamente, então se move de volta em direção a 0.
4. No ponto E, a tangente é horizontal, então deve ser 0 (ponto F).
5. Após o ponto E, aumenta a uma taxa crescente, então deve estar acima do eixo x e aumentando.
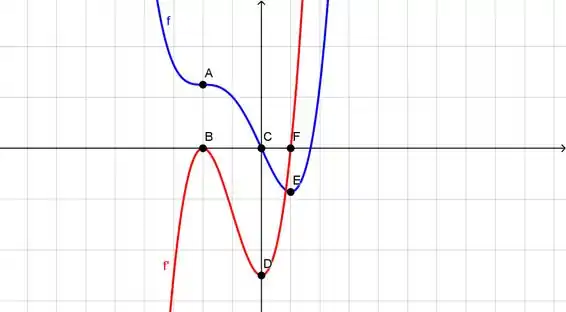
Resposta
