Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 26
Trace a curva para descobrir onde a curva intercepta ela mesma. Depois, encontre as equações de ambas as tangentes nesse ponto.
Passo 1
Eaee, belezinha??
Bom... a questão é bem direta aqui... queremos traçar a curva parametrizada pelas seguintes equações:
Depois de traçar essa curva, queremos encontrar o ponto onde a curva intercepta ela mesma e, com isso, calcular as tangentes nesse ponto.
Isso mesmo... “as tangentes”. Pois como há interceptação, então podemos ter mais de uma tangente.
Lembrando que para calcular a tangente em um ponto a gente aplica a derivada, que vai ser o nosso coeficiente angular:
Depois que calcularmos a derivada, aplicaremos na equação da reta para descobrir a tangente naquele ponto:
Onde representa as coordenadas de um ponto conhecido.
Agora bora lá!! 😉
Passo 2
Bom... utilizando uma ferramenta gráfica, obtemos:
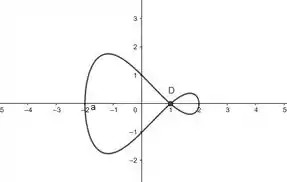
O ponto em que ele intersecta a si mesmo então é , certo?
Ou seja, quando ou .
Ahh... outra coisa: Por esse gráfico a gente pode verificar os pontos conhecidos.
Em uma tangente teremos o ponto e na outra teremos o ponto .
Isso significa que basta a gente encontrar uma equação da reta tangente para depois só mudar o sinal hehe.
Quer saber como?? Bora lá!!
Passo 3
Agora vamos calcular a derivada para depois substituirmos pelos valores de :
Aplicando a soma de derivadas:
Sabemos que a derivada do seno é o cosseno. E que a derivada do cosseno é o seno negativo. Assim, temos:
Beleza, vamos substituir os pontos...
Passo 4
Para temos:
E pra :
Esses são os coeficientes angulares das nossas retas tangentes.
Passo 5
Montamos as equações agora da reta tangente:
Assim, alterando o sinal, encontramos a outra reta tangente:
Prontinho galera!!