Encontre os pontos na curva dada onde a reta tangente é horizontal ou vertical.
Passo 1
Eaee, beleza?? Bom... o enunciado nos deu a seguinte equação polar:
Queremos encontrar os pontos na curva dada onde a reta tangente é horizontal ou vertical.
Para calcular a inclinação da reta tangente basta usar a fórmula:
Para achar os pontos onde a tangente é horizontal é necessário que:
e
E, para achar os pontos onde a tangente é vertical, é necessário que:
e
Aahh.. vamos precisar saber também da relação entre coordenadas polares e cartesianas. Se liga que o ponto pode ser dado tanto por coordenadas quanto por coordenadas :
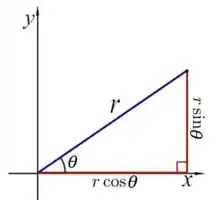
Agora bora aplicar!! 😉
Passo 2
Para começar, vamos achar o que é .
Pela figura do passo 1, podemos ver que trata-se de:
Substituindo
Agora achando , pela figura, temos:
Substituindo , temos:
Passo 3
Para achar as tangentes horizontais, vamos primeiro derivar :
Igualando a zero, temos:
Passando o para o outro lado da equação:
Essa igualdade só ocorre quando , e isso ocorre nos ângulos
Passo 4
Para achar as tangentes verticais, vamos derivar :
Igualando a zero
Substituindo , temos:
Utilizando a mudança de variável
Resolvendo a equação por Bhaskara
Substituindo :
Simplificando a fração por :
E
Agora vamos analisar um pouco...
Passo 5
Para o primeiro valor de , qual o que faz ?
Neste caso, não existem valores de reais, porque , e .
Então vamos focar no segundo valor de .
Qual o que faz ?
Para não ficarmos usando isso toda hora, vamos nomear esse valor de
Mas o só cobre metade do circulo trigonométrico e existe outro que satisfaz essa condição e esse ângulo é o suplementar de então:
Passo 6
Como não tivemos ângulos que tiveram e , todos os ângulos que achamos serão pontos críticos.
Para finalizar agora e sabermos os pontos exatos, basta calcular para cada achado.
Para tangentes horizontais, com :
E, com , temos:
Então os pontos que tem tangentes horizontais, no formato são e .
Passo 7
Para tangentes verticais, com , temos:
E, com , temos:
Então os pontos que tem tangentes verticais, no formato são
e
Resposta
Horizontais: e .
Verticais: e onde .