Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 40

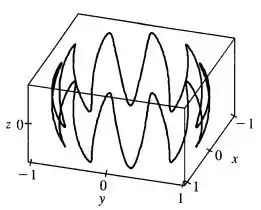
Trace a curva com equações paramétricas

x = 1 - 0,25 cos 2 ⁡ 10 t cos ⁡ t   ,           y = 1 - 0,25 cos 2 ⁡ 10 t s e n   t   ,           z = 0,5 cos ⁡ 10 t

Explique a aparência da curva, mostrando que ela está em uma esfera.

Passo 1

Eaee, tudo tranquilo?? Bom... o enunciado nos deu as seguintes equações paramétricas que descrevem uma curva:

x = 1 - 0,25 cos 2 ⁡ 10 t cos ⁡ t

y = 1 - 0,25 cos 2 ⁡ 10 t s e n   t  

z = 0,5 cos ⁡ 10 t

Queremos explicar a aparência da curva, mostrando que ela está em um cone.

Mas como fazemos isso???

Pra mostrar isso, vamos utilizar x , y e z das equações paramétricas e tentar chegar a:

x 2 + y 2 + z 2 = k 2

sendo k uma constante qualquer.

Ou seja, vamos substituir duas equações paramétricas na equação da esfera e vamos verificar se bateu o resultado!! Se bater, então está provado!! Aí é só a gente plotar depois 😉

Passo 2

Vamos pegar as equações paramétricas e somar o quadrado delas:

x 2 + y 2 + z 2 = 1 - 0,25 cos 2 ⁡ 10 t cos 2 ⁡ t + 1 - 0,25 cos 2 ⁡ 10 t   s e n 2   t + 0,5 2 cos 2 ⁡ 10 t

Colocando os termos comuns em evidência:

x 2 + y 2 + z 2 = 1 - 0,25 cos 2 ⁡ 10 t cos 2 ⁡ t + s e n 2   t + 0,25 cos 2 ⁡ 10 t

Sabemos de uma identidade trigonométrica que cos 2 ⁡ t + s e n 2   t = 1 , portanto:

x 2 + y 2 + z 2 = 1 - 0,25 cos 2 ⁡ 10 t + 0,25 cos 2 ⁡ 10 t

x 2 + y 2 + z 2 = 1

Veja que o nosso resultado foi 1 , ou seja, uma constante!!!

Galera, com a ajuda de um computador, vamos traçar a curva:

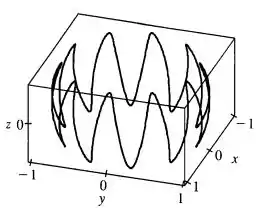
Realmente, a curva parece estar contida numa esfera de raio 1 .

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize o computador para traçar a curva da equação vetorial dada. Escolha o dom��nio do parâmetro e ponto de vista de forma a garantir que a visualização é verdadeira. r → t = s e nt , s e n2 t , s e
Estabeleça as equações paramétricas para a reta tangente a curva dada pelas equações paramétricas, no ponto especificado. Ilustre traçando o gráfico da curva e da reta tangente em uma mesma tela. x =
Determine se as curvas são lisas(a) r → t = t 3 , t 4 ,t 5 (b) r → t = t 3 + t , t 4 ,t 5 (c) r → t = cos 3 ⁡ t , s e n 3 t
As curvas r → 1 t = t , t 2 , t 3 e r → 2 t = s e nt , s e n2 t , t se encontram na origem. Determine o ângulo de interseção destas com a precisão de graus.
(a) Determine o ponto de interseção das retas tangente à curva r → t = s e nπ t ,2 s e nπ t, cos ⁡ π t No ponto t = 0 e t = 0,5 .(b) Ilustre traçando o gráfico da curva e ambas as tangentes.