Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.1 - Ex. 22
Trace a curva estime visualmente seu comprimento. Use sua calculadora para encontrar o comprimento da curva com precisão de quatro casas decimais.
Passo 1
Vamos traçar a curva, beleza?
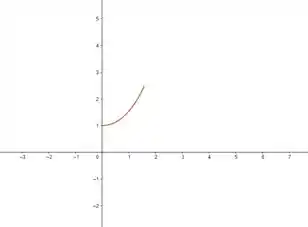
Agora com a curva desenhada, parece uma reta não é? Então, visualmente, poderíamos estimar o comprimento como sendo a hipotenusa do triângulo retângulo de base de zero a dois. O
Passo 2
Vamos tentar medir usando a fórmula de comprimento agora, ok?
Vamos encontrar a derivada para substituir na fórmula, blz.
Substituindo,
Com a ajuda da calculadora,
Resposta
Exercícios de Livros Relacionados
24- Circunferência de um círculo Estabeleça uma integral para determinar a circunferência de um círculo de raio r centrado na origem. Você aprenderá a calcular a integral na Seção 8.3
29- Aproxime o comprimento do arco de um quarto de círculo unitário ( que é π / 2 ) pelo cálculo do comprimento da aproximação poligonal com n = 4 segmentos (veja a figura a seguir).
Determine os comprimentos das curvas nos Exercícios 17-20.19. y = x 2 - ln x / 8 , 1 ≤ x ≤ 2
Determine os comprimentos das curvas nos Exercícios 17-20.17. y = x 1 / 2 - 1 3 x 3 2 , 1 ≤ x ≤ 4
Determine os comprimentos das curvas nos Exercícios 17-20.20. x = ( y 3 / 12) + ( 1 / y ) , 1 ≤ y ≤ 2