Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.2 - Ex. 63

Se a curva x = t + t 3           y = t - 1 t 2             1 ≤ t ≤ 2

girar em torno do eixo x , estime a área da superfície resultante com precisão de três casas decimais.

Passo 1

Precisamos escrever uma integral que represente a área da superfície obtida pela rotação da curva dada ao redor do eixo x .

Sabemos que a área de uma superfície é

S = ∫ a b 2 π y   d s

Sendo que

d s =   d x d t 2 + d y d t 2

Vamos primeiro dar uma olhada na região que precisamos trabalhar:

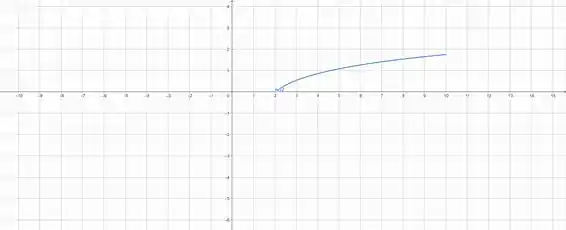
A gente quer encontrar a integral que é da área da superfície de um solido gerado ao rotacionar essa figura em torno do eixo x .

Para fazer isso, a gente precisa calcular as derivadas de:

x = t + t 3           y = t - 1 t 2

E montar a integral. O cálculo da integral em si, será feito utilizando uma calculadora, muito provavelmente essa integral não é possível de resolver na mão, vamos montar e ver se isso é verdade.

Passo 2

Temos então que:

x = t + t 3

Então

d x d t = 1 + 3 t 2

Agora vamos para y :

y = t - 1 t 2

Podemos reescrever como:

y = t - t - 2

d y d t = 1 + 2 t - 3

Vamos agora montar a integral, veja que o intervalo de integração é o de t que nos foi dado, já que estamos trabalhando em função de t , não precisamos encontrar o intervalo pelos meios que normalmente fazer, apenas utilizar o já dado:

S = ∫ 1 2 2 π t - 1 t 2 1 + 3 t 2 2 + 1 + 2 t - 3 2 d t

Desenvolvendo os produtos notáveis:

S = ∫ 1 2 2 π t - 1 t 2 2 + 4 t - 6 + 4 t - 3 + 6 t 2 + 9 t 4 d t

Aqui a gente só consegue resolver utilizando um software, o resultado é:

S ≈ 59.101

Resposta

S ≈ 59,101

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre as áreas das regiões nos Exercícios 9-18Dentro do círculo r = 4 sen ⁡ θ e abaixo da reta horizontal r = 3 c o s s e cθ .
Encontre a área da região sombreada na figura a seguir.Parece que, se o gráfico de r = t gθ ,- π 2θπ 2 , poderia ser assintótico às retas x = 1 e x = - 1 . Sim ou não? Justifique sua resposta.
Circunferências dos círculosComo é usual diante de uma nova fórmula, é uma boa ideia testá-la em objetos familiares para ter a certeza de que ela fornece resultados consistentes com a experiência pass
r = f θ contra r = 2 f ( θ ) Alguma coisa pode ser dita sobre os comprimentos relativos das curvas r = f θ ,α ≤ θ ≤ β , e r = 2 f θ ,α ≤ θ ≤ β ? Justifique sua resposta.
Valor médioSe f é continua, o valor médio da coordenada polar r sobre a curva r = f θ ,α ≤ θ ≤ β , com relação a θ é dado pela formula: r m = 1 β - α ∫ α β f θ d θ Utilize essa formula para encontrar