Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 28
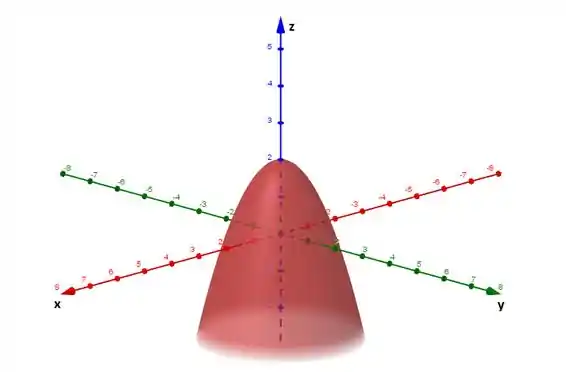
Esboce o gráfico da função.
Passo 1
Olá, meu amigo. Vamos resolver essa atividade juntos?
Queremos determinar o gráfico da função:
Para esboçarmos o gráfico de uma função de duas varáveis precisamos primeiramente encontrar as curvas de nível desta função.
Para isso façamos:
A partir disso, iremos analisar alguns pontos dessa função. Iremos analisar o seu comportamento para diferentes valores de , isso nos dará a noção de como é o formato da curva de nível e consequentemente nos dirá como é o formato da nossa figura.
Também deveremos encontrar os pontos de intersecção com os eixos. Para isso, deveremos zerar duas variáveis, e assim encontrarmos onde a nossa figura encontra o eixo da variável que sobrou.
Passo 2
Se analisarmos o domínio dessa função, veremos que nunca pode ser maior que 2, pois se isso acontecer teremos um resultado negativo e dois números ao quadrado no conjunto dos reais nunca é negativo.
Então tendo em mente essa restrição vamos escolher alguns valores para :
, , e .
Desta forma obtemos as seguintes curvas de nível:
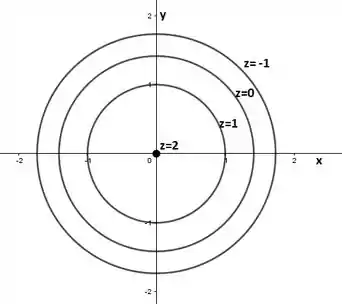
Então podemos pensar que a nossa figura se inicia em , e é uma circunferência que vai crescendo a medida que aumenta.
Os pontos de intersecção com os eixos são:
Para o eixo :
Para o eixo
E em
Passo 3
Desta forma o gráfico de é:
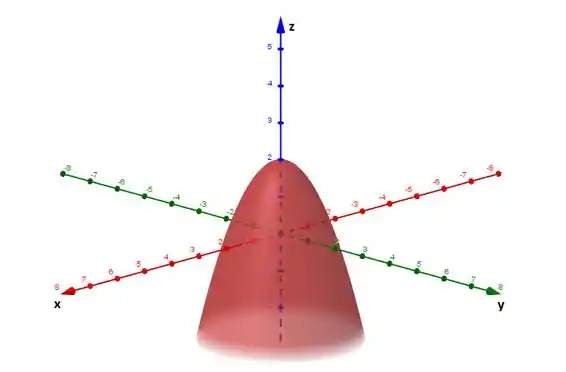
Resposta
