Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.8 - Ex. 34
Trace na mesma tela as primeiras somas parciais da série , com a função-soma . Em que intervalo essas somas parciais parecem estar convergindo para ?
Passo 1
Beleza, galera? O enunciado pede para analisarmos o intervalo que as somas parciais convergem para a partir do traçados no gráfico. Ou seja, teremosa várias linhas referentes a cada soma parcial da série, assim como o traçado da linha da função.Poderemos então ver o que acontece a cada soma parcial. Então o primeiro passo é traçar os gráficos, e então iremos analisar os resultados.
Passo 2
Para calcular as somas parcias temos que saber que uma série é uma soma de infinitos termos da seguinte forma:
Porém, como queremos uma soma parcial, significa que faremos essa soma até uma valor de qualquer. Faremos essa soma para alguns valores de e iremos traçar os gráficos. Veja:
Vamos traçar as seguintes funções:
Em azul claro:
Em cinza claro:
Em ciano:
Em roxo
Em pink:
Em azul
n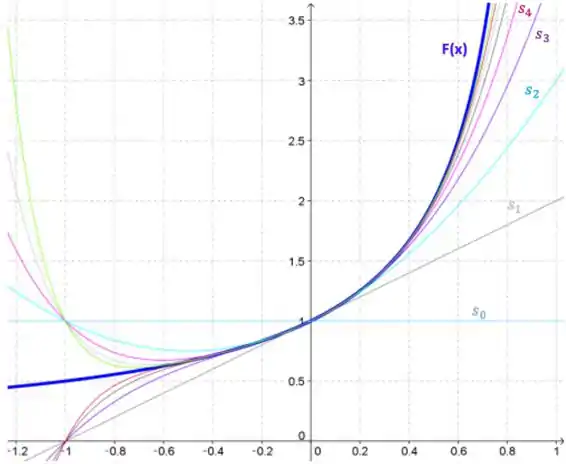
A curva mais grossa (em azul) é
Passo 3
Agora observe o gráfico. é uma reta horizontal, já é uma reta oblíqua que se aproxima de pelo menos em torno de . E à medida que vamos aumentando o número de termos das somas parciais, as funções vão convergindo cada vez mais para
Até , conseguimos ver que o gráfico parece convergir aproximadamente no intervalo . Mas sabemos que o intervalo de convergência dessa série é , então, se acrescentássemos mais e mais gráficos de somas parciais, poderíamos visualizar isso.
Resposta
Questão teórica.