- Mostre que a função definida por
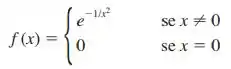
não é igual à sua série de Maclaurin.
- Trace a função na parte (a) e comente seu comportamento próximo a origem.
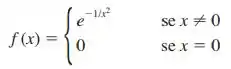
não é igual à sua série de Maclaurin.
Passo 1
- Neste exercício a gente vai começar escrevendo nossa função como uma série exponencial para depois verificar se ela atende a definição de série de Maclaurin.
- No gráfico
Para construir essa série, podemos usar a série da exponencial
Então adequando para a equação do enunciado, teríamos:
E isso vale para .
Passo 2
Mas se nós olharmos para a definição da série de Maclaurin
Temos que a função foi definida no enunciado por
Agora vamos usando a definição de derivada, temos que
Temos uma indeterminação . Galerinha, já adianto que se aplicarmos L’Hospital aqui direto, ainda não vamos conseguir resolver esse limite. Então vamos manipular um pouco essa equação para achar esse limite
Agora temos uma indeterminação , aplicando L’Hospital
E se calcularmos as próximas derivadas teremos sempre o mesmo resultado, fazendo a série de Maclaurin ser igual a
Portanto o único caminho de encontrar a série é utilizando a série da exponencial, mas não conseguimos construir a série por ela mesma.
Passo 3
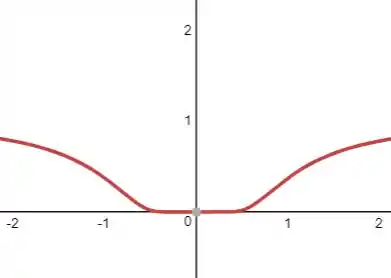
Analisando a parte , temos que , a nossa , apesar de não estar definida neste ponto. Contudo, o enunciado nos diz que a nossa , tornando a função continua.
Resposta
Ei, a resposta está no passo a passo :)