Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 62
62. Um trângulo possui lados e , e ângulo (como no exercício 59). Determine o seno do ângulo utilizando a lei dos senos.
Passo 1
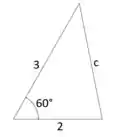
Usando a lei dos cossenos encontramos que . (Ver exercício 59)
Agora só precisamos jogar na fórmula. O ângulo é o ângulo oposto ao lado .
Resposta
Exercícios de Livros Relacionados
Encontre os valores das funções nos Exercicios 47-50.47. cos 2 π 8
45. Avalie cos π 12 .
Encontre os valores das funções nos Exercicios 47-50.50. sen 2 3 π 8
Encontre os valores das funções nos Exercicios 47-50.48. cos 2 5 π 12
Para os Exercícios 51-54 encontre o ângulo θ , onde 0 ≤ θ ≤ 2 π .52. sen 2 θ = cos 2 θ