Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.8 - Ex. 74

Transforme a integral imprópria dada em uma integral própria fazendo a substituição u dada e, então, aproxime a integral própria pela regra de Simpson com n = 10 subdivisões. Arredonde sua resposta para três casas decimais.

∫ 0 1 sin ⁡ x 1 - x d x ; u = x

Passo 1

Bom galera, vamos começar mudando a variável da nossa integral:

∫ 0 1 sin ⁡ x 1 - x d x

Vamos chamar:

u = 1 - x

d u = - 1 2 1 - x d x

Mudando a integral ficamos com:

∫ 0 1 2 sin ⁡ ( 1 - u 2 ) d u

Passo 2

Belezinha, agora vamos calcular a integral pela aproximação de Simpson, S 10 :

S n ≈ b - a 3 n ( y 0 + 4 y 1 + 2 y 2 + 4 y 3 + … + 2 y n - 2 + 4 y n - 1 + y n )

Vamos calcular pela tabela:

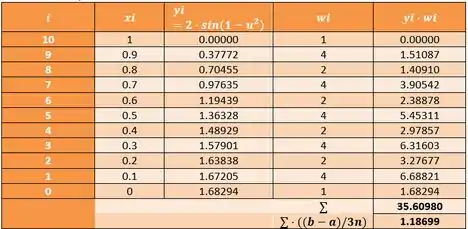
Passo 3

Logo, encontramos o resultado aproximado da nossa integral:

∫ 0 1 sin ⁡ x 1 - x d x = 1 . 18699

Resposta

1.18699

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4. Calcule ∫ 1 ∞ 1 x α d x , onde α é um numero real.
Calcule: ∫ 0 + ∞ x 1 + x 4d x
Determine m para que ∫ - ∞ + ∞ f xd x = 1 onde f x = ms ex ≤ 3 0s ex3
Calcule: ∫ - ∞ - 1 1 x 3d x
Calcule: ∫ 0 - ∞ x e - x 2d x