Em cada parte, combine a equação com um dos gráficos dados.
(a)
(b)
(c)
(d)
(e)
(f)
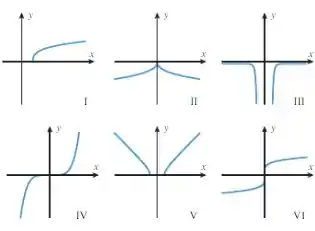
Passo 1
Para cada uma das funções vamos ter que identificar algum ponto chave que nos indique a característica principal da função e, assim, conectar a um dos gráficos. Vamos lá!
Passo 2
(a)
Aqui, nós podemos lembrar do gráfico de :
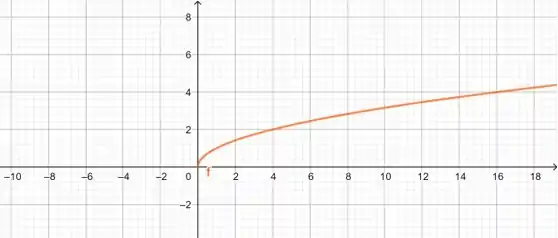
Dessa forma, podemos pensar em um gráfico parecido. A principal diferença será que em nós não temos valores negativos de , já em nós teremos! Isso porque todo número real possui essa raiz quinta.
O gráfico que mais se assemelha ao gráfico de , possuindo valores negativos de é o VI:
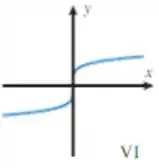
A outra diferença perceptível é um maior achatamento da curva. Isso, inclusive é discutido pelo livro ao falar dos gráficos dessa família. Tudo certo por aqui.
Passo 3
(b)
Aqui, vamos lembrar do gráfico de :
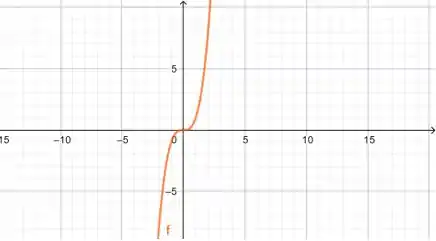
Como temos um , a diferença é que a curva vai ser mais achatada que a de .
No caso, podemos ver que o gráfico que mais se assemelha a esse é o IV:
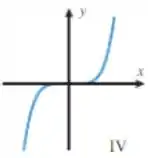
Passo 4
(c)
Agora, vamos lembrar do gráfico de :
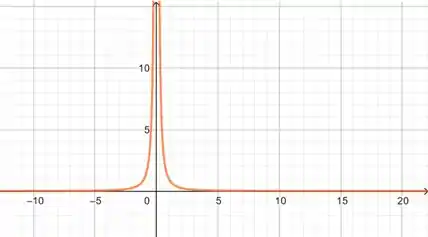
Vamos ter algo parecido com ele, a diferença é que será mais achatado por conta da potência de e estará refletido em torno de por conta do sinal de na frente.
Dessa forma, a que mais se assemelha é é a III:
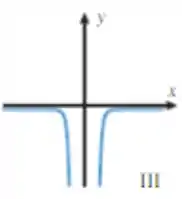
Passo 5
(d)
Vamos lembrar do gráfico de , que aparece no livro, na figura 0.3.12.
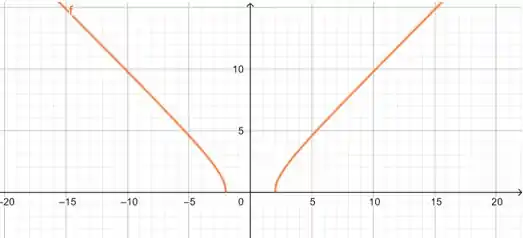
E o gráfico que mais se assemelha é o V:
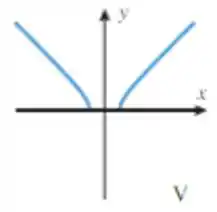
Passo 6
(e)
Cara, se você reparar nessa equação, temos dentro da raiz, certo? E você lembra que quando diminuímos ao da função, deslocamos o gráfico em unidades para a direita.
E o único gráfico que está deslocado para a direita é o I:
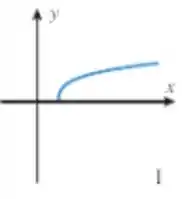
Passo 7
(f)
Podemos reescrever dessa forma:
Vamos lembrar do gráfico de , que também aparece no livro:
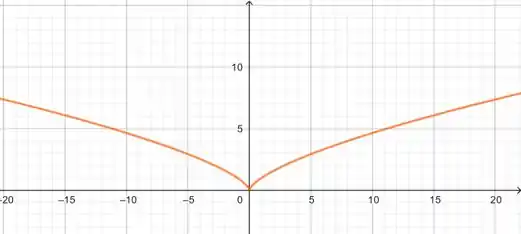
Mas, como temos um sinal negativo na frente da nossa função, isso reflete o gráfico pelo eixo .
O gráfico que mais se assemelha ao resultado disso é o II:
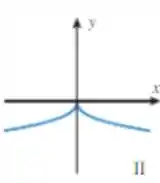
Resposta
(a) VI
(b) IV
(c) III
(d) I
(e) V
(f) II