Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 61a
é um triângulo retângulo com o ângulo reto em . Os lados opostos aos ângulos e são e , respectivamente.
Determine e se e
Passo 1
E aí, galera! Vou te mostrar como fica o esboço desse desenho:
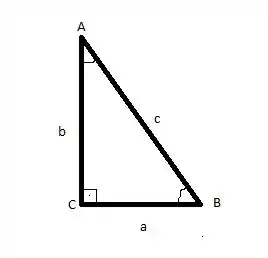
Agora, nessa questão ele te deu alguns dados. A figura, a partir dos dados, é essa:
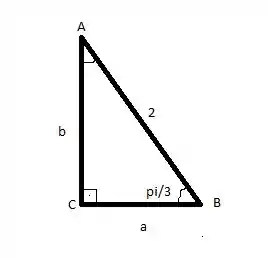
Vamos usar alguma das relações trigonométricas pra descobrir esses valores. Elas são:
seno:
cosseno:
tangente:
Passo 2
Aqui, vamos ver o que a gente vai usar a partir dos dados. Ele te deu um ângulo (), então a relação trigonométrica vai ser usada a partir dele. Então, em relação a B, b é o cateto oposto, a é o cateto adjacente e c é a hipotenusa. Como ele deu o c (hipotenusa), vamos usar as relações que tem hipotenusa, então:
- descobrir o a usando cosseno
- descobrir o b usando seno
Agora são as continhas:
- . A gente sabe que
- . A gente sabe que
(ali eu passei o 2 do denominador do lado direito para o lado esquerdo como multiplicação)
Resposta
e