Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 48
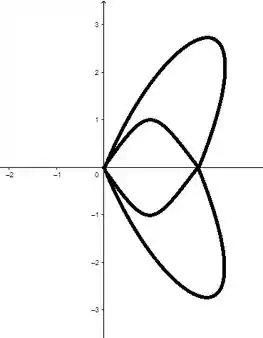
A figura mostra o gráfico de como uma função de em coordenadas cartesianas. Use-o para esboçar a curva polar correspondente.
Passo 1
Olá, meu amigo. Vamos resolver juntos essa atividade aqui.
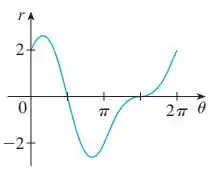
A gente tem o gráfico:
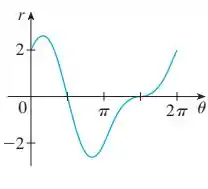
E esse gráfico é de uma função . A partir dele, a gente precisa construir o gráfico polar dessa função.
Nas equações polares o representa a distância do ponto até a origem e o a angulação deste ponto em relação ao eixo no plano.
Nesta questão vamos ter que pegar uma aproximação dos valores e fazer o esboço do gráfico com eles a medida que o ângulo aumenta.
A gente precisa ter em mente aqui que o segredo para montarmos o gráfico é acompanhar o crescimento e o decrescimento do raio em relação ao ângulo, pois é isso que o gráfico mostra.
Passo 2
Nessa função o começa em 2 aumenta mais ou menos até o na metade do primeiro quadrante e no fim do quadrante diminui até o .
Depois diminui até na metade do segundo quadrante e aumenta até no final do quadrante.
No terceiro quadrante ele vai aumentando devagar até chegar no .
E no quarto quadrante vai aumentando devagar até chegar no .
No plano vai ficar mais ou menos assim:
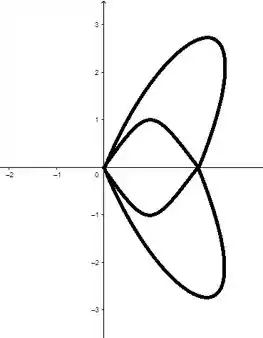
Resposta
