Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.3 - Ex. 27
Usando o método das camadas cilíndricas, monte uma integral (mas não a calcule) para o volume do sólido gerado quando a região é girada em torno
da reta e da reta .
é a região delimitada pelos gráficos , e .
Passo 1
Bom galera, vamos começar delimitando a área:
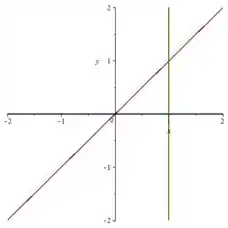
Passo 2
Belezinha, vamos calcular o volume integrando primeiro pelo eixo , então temos o nosso raio e o intervalo é , e a altura é , logo nossa integral vai ficar:
Passo 3
Show de bolinhas, agora integrando pelo eixo , a gente tem o raio , no intervalo , a altura do nosso cilindro é , assim o volume é dado por:
Resposta
Exercícios de Livros Relacionados
Se um fluido entra em um tanque semiesférico com raio de 3m , a uma taxa de 0,5m 3 / m i n , com que velocidade estará subindo quando a profundidade for de 1,5m ? [Sugestão Veja o exercicio 55 .]
A figura a seguir mostra as dimensões de uma pequena lâmpada em 10 pontos igualmente espaçados.(a) Use fórmulas de Geometria para fazer uma primeira estimativa do volume englobado pela parte de vidro
A figura abaixo mostra uma calota esférica de raio ρ e altura h cortada de uma esfera de raio r . Mostre que o volume V da calota pode ser expresso como: V = 1 3 π h 2 ( 3 r - h ) V = π h 6 3 e 2 + h
Encontre o volume da cunha descrita no Exercício 61 por fatiamento perpendicular ao eixo x .
Em 1635, Bonaventura Cavalieri, um aluno de Galileu, estabeleceu o seguinte resultado, chamado princípio de Cavalierri: Se dois sólidos tiverem a mesma altura, e se as áreas de suas seções transversai