Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.3 - Ex. 62

A região limitada abaixo pelo eixo x e acima pela parte de y = sin ⁡ x de x = 0 a x = π gira em torno do eixo x . Encontre o volume do sólido resultante.

Passo 1

Bom galera, vamos começar delimitando a área:

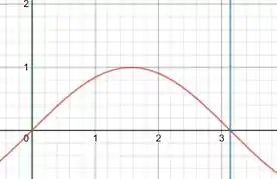
Passo 2

Belezinha, vamos começar calculando o volume do sólido de revolução, que é dado pela integral:

V = π ∫ a b x 2   d x

→ V = π ∫ 0 π sin 2 ⁡ x   d x

Pra facilitar nossa vida a gente usa uma identidade trigonométrica, fica assim:

→ V = π ∫ 0 π 1 - cos ⁡ 2 x 2 d x

→ V = π 2 ∫ 0 π 1 - cos ⁡ 2 x d x

Passo 3

Show de bolinhas, agora vamos resolver a nossa integral e pronto:

V = π 2 ∫ 0 π 1 - cos ⁡ 2 x d x

→ V = π 2 x - 1 2 sin ⁡ 2 x 0 π

→ V = π 2 π = π 2 2

Resposta

π 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcula a integral ∫ 0 π 4 1 - cos ⁡ 4 θd θ
Calcula a integral ∫ cos ⁡ π x cos ⁡ 4 π xd x
Calcula a integral ∫t g 2 x sec 4 ⁡ x d x
Calcula a integral ∫ t g 5 x sec 3 ⁡ xd x
Calcula a integral ∫ 0 π 2t g 4 td t