Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.10 - Ex. 18b
Usando o teorema , o que se pode afirmar sobre o campo vetorial dado?
b) em
Passo 1
Pelo teorema , se , podemos afirmar que o campo é conservativo, e que admite uma função potencial .
Passo 2
Vamos então calcular para verificar polo teorema se o campo é conservativo.
Então basta fazermos o seguinte:
Passo 3
Aplicando a formula cima em temos:
Passo 4
Temos agora que analisar o domínio. Para isso podemos plotar um gráfico do domínio.
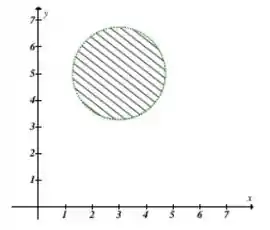
Podemos observar que não contém a origem e que é simplesmente conexo. Portanto podemos afirmar que o campo é conservativo em , e que admite uma função potencial .
Resposta
Campo vetorial conservativo em , admite uma função potencial .
Exercícios de Livros Relacionados
Determine (a) o rotacional e (b) o divergente do campo vetorial. F x , y , z = 1 x 2 + y 2 + z 2 xi + yj + zk
b) Calcule ∫ C 2 x y 3 - y 2 cos x d x + 1 - 2 y sin x + 3 x 2 y 2 d y , onde C é o arco da parábola 2 x = π y 2 , de P 1 = 0,0 até P 2 = π 2 , 1 .
Considere a integral de linha ∫ C y 2 - x y d x + k x 2 - 4 x y d y . b) Calcule o valor da integral de A = 0,0 a B = 1,1 para o valor de k encontrado em a).
Caso exista encontre uma função potencial para V x , y = 2 x y 3 - y 2 cos x , 1 - 2 y sin x + 3 x 2 y 2 .
Verifique que as seguintes integrais independem do caminho e calcule seus valoresa) ∫ 1 , - 2 3,4 y d x - x d y x 2