Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.16 - Ex. 17
Usar o teorema da divergência para calcular a integral da superfície dada.
Sendo a parte da esfera abaixo do plano , com normal exterior.
Passo 1
O teorema da divergência relaciona uma integral tripla sobre um sólido e uma integral dupla sobre a superfície fronteira deste sólido.
Seja um sólido no espaço, limitado por uma superfície orientável . Se é a normal unitária exterior a e se é uma função vetorial contínua que possui derivadas parciais de ordem contínuas em um domínio que contém , então
Assim tendo introduzido formalmente o nosso teorema, podemos agora começar a aplica-lo e começar a nos familiarizarmos com ele.
Passo 2
Olhando para nossa integral dada, temos que , assim o divergente de
Com relação a nossa superfície dada, temos uma esfera centrada na origem do nosso sistema e de raio . Assim o que precisamos fazer, é definir os limites de integração da nossa esfera, sabendo até que vai devemos varia nosso . Vamos fazer e vê o que acontece.
Primeiro vamos parametrizar nossa esfera para facilitar o nosso entendimento sobre os limites de integração.
As duas primeiras coisas que até o momento é bem tranquilo, é que e , mas o quanto varia .
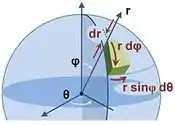
No plano e tomando , temos que . Assim temos . Agora estamos prontos para integrar.
Com a parametrização que fizemos, não podemos esquecer que
Passo 3
Assim aplicando o teorema da divergência, temos
Assim temos
Que é exatamente o que estavam esperando.