Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.5 - Ex. 44a
44. a) Use uma calculadora para tabular até quatro casas decimais, valores de
Quando . A que o quociente parece tender quando h se aproxima de 0?
Passo 1
Nessa questão não há mistério algum, basta calcular o valor do quociente para os vários valores de h, o enunciado ainda facilita nossa vida dizendo que pode usar calculadora.
Depois basta ver a que número o quociente tende quando h se aproxima de 0.
Passo 2
Resultado do quociente para os valores de h:
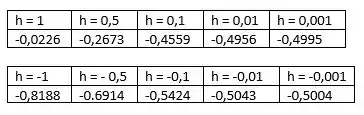
Vemos que o quociente tende a -0,5 quando .
Resposta
Analisando os resultados obtidos podemos perceber que quando h se aproxima de zero o quociente tende a -0,5.
Exercícios de Livros Relacionados
Calcule f ' x . f x = 3 x + 1 x
Calcule f ' x . f x = x 3 + x
Calcule f ' x . f x = 2 x 3
Calcule f ' x . f x = 3 x + x
Calcule f ' x . f x = 2 3 x 3 + 1 4 x 2