Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.5 - Ex. 4b

b) Use a) para calcular a área da região limitada pelo eixo y , pelas retas y = 1 ,   y = 3 e pela curva x = y 2 .

Passo 1

Inicialmente, vamos procurar desenhar a região dada.

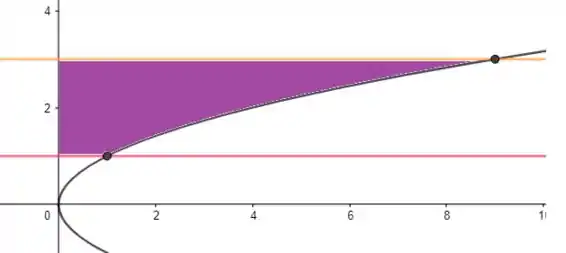
Pela propriedade da letra a), sabemos que a área da figura poderá ser calculada como

á r e a = ∮ ∂ D x   d y

Ou seja, F → x , y = 0 ,   x . Então, vamos procurar especificar nosso caminho.

Passo 2

á r e a = ∮ C 1 x   d y + ∮ C 2 x   d y + ∮ C 3 x   d y + ∮ C 4 x   d y

onde:

  • C 1 é o caminho r t = t 2 ,   t com 1 ≤ t ≤ 3 ;
  • C 2 é o caminho r t = 9 - t ,   3 com 0 ≤ t ≤ 9 ;
  • C 3 é o caminho r t = 0 ,   3 - t com 0 ≤ t ≤ 2 ;
  • C 4 é o caminho r t = t ,   1 com 0 ≤ t ≤ 1 .

Veja a figura abaixo que ilustra melhor essas escolhas de caminho.

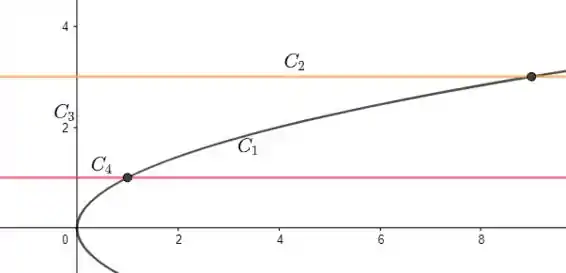
Passo 3

Então, calculando cada integral:

  1. I 1 = ∮ C 1 x   d y = ∫ 1 3 F r t ⋅ r ' t   d t I 1 = ∫ 1 3 0 , t 2 ⋅ 2 t ,   1   d t = ∫ 1 3 t 2 d t I 1 = t 3 3 1 3 = 26 3

  2. I 2 = ∮ C 2 x   d y = ∫ 0 9 F r t ⋅ r ' t   d t I 2 = ∫ 0 9 0 ,   9 - t 2 ⋅ - 1 ,   0   d t = ∫ 0 9 0   d t = 0

  3. I 3 = ∮ C 3 x   d y = ∫ 0 2 F r t ⋅ r ' t   d t I 3 = ∫ 0 2 0 ,   0 2 ⋅ 0 ,   - 1 = 0

I 4 = ∮ C 4 x   d y = ∫ 0 1 F r t ⋅ r ' t   d t I 4 = ∫ 0 1 0 , t 2 ⋅ 1,0 = 0

Passo 4

Assim, segue que

á r e a = I 1 + I 2 + I 3 + I 4 á r e a = 26 3 + 0 + 0 + 0 á r e a = 26 3

Resposta

A área vale 26 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja C uma curva fechada, orientada positivamente, limitando uma região do plano x y , de área A . Verifique que se a 1 ,a 2 ,a 3 , b 1 , b 2 ,b 3 são constantes reais, então ∮ a 1 x + a 2 y + a 3 d x
Determine ∮ C x 2 + y + 2 x y 3 d x + 5 x + 3 x 2 y 2 + yd y onde C é a reunião das curvas C 1 ,C 2 e C 3 dadas por C 1 : x 2 + y 2 = 1 ,y ≥ 0 ; C 2 : x + y + 1 = 0 , - 1 ≤ x ≤ 0 ; C 3 : x - y - 1 = 0
Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.a. ∮ C y 2 d x + x 2 d y C é a fronteira do quadrado D = - 1,1 × - 1,1
Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.b. ∮ C 3 x 2 + y d x + 4 y 2 d y C é a fronteira do triangulo de vértices. 0,0 , 1,0 , 0,2
Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.c. ∮ C e x - 3 y d x + e y - 6 x d y C é a elipse de equação x 2 + 4 y 2 = 1