Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.5 - Ex. 6b

Seja F x , y = - y x 2 + y 2 , x x 2 + y 2 + 3 x um campo vetorial em R 2 . Calcule a integral de linha do campo F ao longo das curvas C 1 e C 2 , orientadas no sentido anti-horário, onde:

  1. C 1 é a circunferência de equação x 2 + y 2 = 4 .

C 2 é a fronteira do retângulo R = x , y ∈ R 2 : - π ≤ x ≤ π ,   - 3 ≤ y ≤ 3 .

Passo 1

  1. A gente pode aplicar o teorema de Green, mas não no conjunto dado.

Podemos, por exemplo, tomar o conjunto D abaixo.

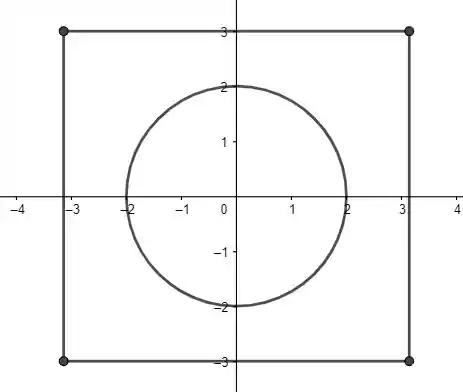
onde percorremos o retângulo no sentido anti-horário e o círculo no sentido horário. Assim, o conjunto D será o retângulo menos o círculo, de modo que 0,0 não estará no interior de D . Sendo assim,

∮ C 2 ∪ C 1 - F 1   d x + F 2   d y = ∬ D ∂ F 2 ∂ x - ∂ F 1 ∂ y   d x   d y

Primeira coisa que devemos fazer é calcular as derivadas:

∂ F 2 ∂ x = ∂ ∂ x x x 2 + y 2 + 3 x ∂ F 2 ∂ x = y 2 - x 2 x 2 + y 2 2 + 3

Também,

∂ F 1 ∂ y = ∂ ∂ y - y x 2 + y 2 ∂ F 1 ∂ y = y 2 - x 2 x 2 + y 2 2

Logo,

∮ C 2 ∪ C 1 - F 1 d x + F 2 d y = ∬ D y 2 - x 2 x 2 + y 2 + 3 - y 2 - x 2 x 2 + y 2 2 d x   d y ∮ C 2 ∪ C 1 - F 1 d x + F 2 d y = ∬ D 3   d x   d y = 3 ∬ D d x   d y

Note que a última integral é simplesmente a área do retângulo – área do círculo!

∮ C 2 ∪ C 1 - F 1 d x + F 2 d y = 3 2 π 6 - π 2 2 = 24 π

Passo 2

Sendo assim, segue que

∮ C 2 F 1 d x + F 2 d y - ∮ C 1 F 1 d x + F 2 d y = 14 π ∮ C 2 F 1 d x + F 2 d y = 14 π + 24 π = 38 π

Resposta

38 π .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3 ) Seja B o conjuntoe seja γ a fronteira de B orientada no sentido anti-horário. Suponha P (x,y) e Q (x, y) de classe C1 num aberto Ω contendo B. Prove que ∮ γ P d x + Q d y= ∬ B ∂ Q ∂ x - ∂ P ∂ yd x
(Teorema de Green para um círculo.) Seja B o círculo de centro na origem e raio r . Seja γ t = r cos ⁡ t , rs e nt , 0 ≤ t ≤ 2 π . Suponha que P e Q sejam de classe C 1 num aberto Ω contendo B . Prove
Seja K o triangulo a seguir e γ a fronteira de K orientada no sentido anti-horário. Sejam P ( x ,y ) e Q ( x ,y ) de classe C 1 num aberto contendo K .Prove que ∮ γ P d x + Q d y = ∫ ∫ K ∂ Q d x - ∂ P
Seja y = f ( x ) de classe C 1 em a , b e tal que f ' x0 em ] a , b [ . Seja K o conjunto a ≤ x ≤ b e f x ≤ y ≤ f a . Sejam P e Q de classe C 1 em um aberto contendo K . Prove que ∮ γ P d x + Q d y =
Seja y = f x de classe C 1 em [ a , b ] e tal que f ' x0 em ] a , b [ . Seja K o conjunto a ≤ x ≤ b e f a ≤ y ≤ f x . Sejam P e Q de classe C 1 num aberto contendo K . Prove que ∮ γ P d x + Q d y = ∬