Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.1 - Ex. 29

Use o cálculo para encontrar a área do triângulo com os vértices dados.

0,0 ,   2 ,   1 ,   - 1 ,   6

Passo 1

Bom galera, nesse exercício queremos encontrar a área do triângulo especificado. Para isso, utilizaremos a seguinte definição

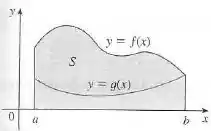
Passo 2

Com dois pontos, podemos encontrar uma equação da reta utilizando a seguinte fórmula

m = ∆ y ∆ x

E

y = m x + n

Dessa forma, entre os pontos ( 0 ,   0 ) e ( 2 ,   1 ) temos a seguinte equação

y = 1 2 x

Entre os pontos ( 0 ,   0 ) e ( - 1 ,   6 ) temos a seguinte equação

y = - 6 x

Entre os pontos ( 2 ,   1 ) e ( - 1 ,   6 ) temos a seguinte equação

y = - 5 3 x + 13 3

Passo 3

Podemos esboçar a região de interesse

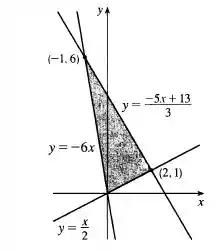
Utilizando a definição do passo 1 , temos

A = ∫ - 1 0 - 5 3 x + 13 3 - - 6 x d x + ∫ 0 2 - 5 3 x + 13 3 - 1 2 x d x

A = ∫ - 1 0 13 3 x + 13 3 d x + ∫ 0 2 - 13 6 x + 13 3 d x

A = 13 x 2 6 + 13 3 x - 1 0 + - 13 x 2 12 + 13 3 x 0 2 = 13 2

Resposta

A = 13 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se x - for a coordenada x do centroide da região que fica sob o gráfico de uma função contínua f , onde a ≤ x ≤ b , mostre que ∫ a b c x + d f x d x = c x - + d ∫ a b f x d x
Um retângulo R com lados a e b foi dividido em duas partes R 1 e R 2 por um arco de parábola que tem seu vértice em um dos cantos de R e passa pelo canto oposto. Encontre os centroides de ambas as reg
Seja R a região que está entre as curvas y = x m e y = x n , 0 ≤ x ≤ 1 , ondem m e n são inteiros com 0 ≤ nm . a Esboce a região R . b Encontre as coordenadas do centroide de R . c Tente encontrar val
Calcule a integral, interpretando-a em termos das áreas. ∫ - 3 0 1 + 9 - x 2 d x
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 2 x d x